Deriving the equation of Centripetal acceleration (using trigonometry)

In this post, we will derive the equation of centripetal acceleration using trigonometry. In a different post, we have done the derivation of the equation of centripetal acceleration using differential calculus.

How to derive the equation of Centripetal acceleration (using trigonometry)

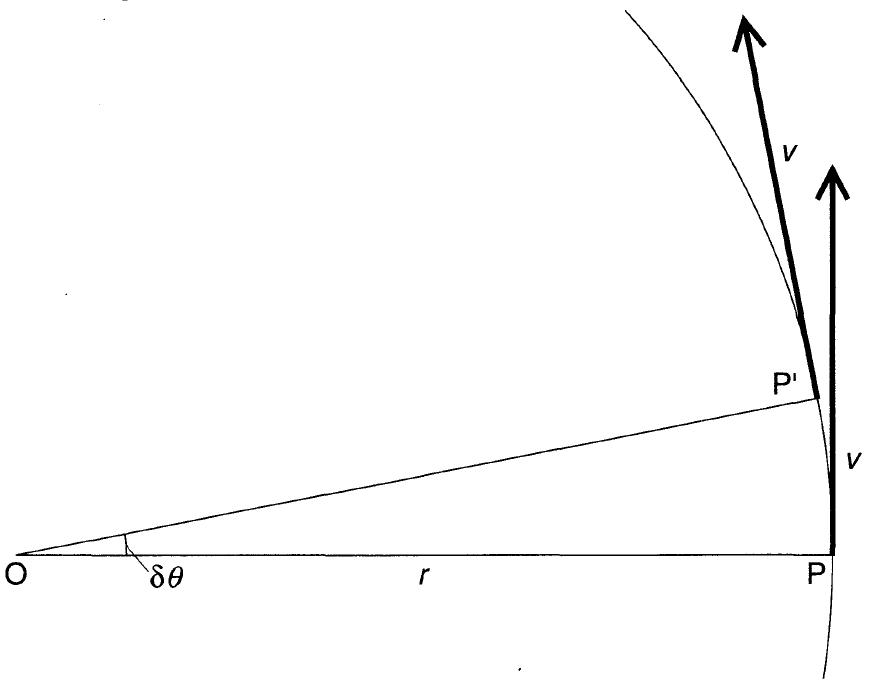
In the above figure (figure 1), a particle is moving in a circle with a steady speed v. The diagram shows how the velocity vector changes direction as the particle moves from P to P’ in time Δt.

In figure 2, the velocity vectors from the previous diagram have been used in a triangle of vectors.

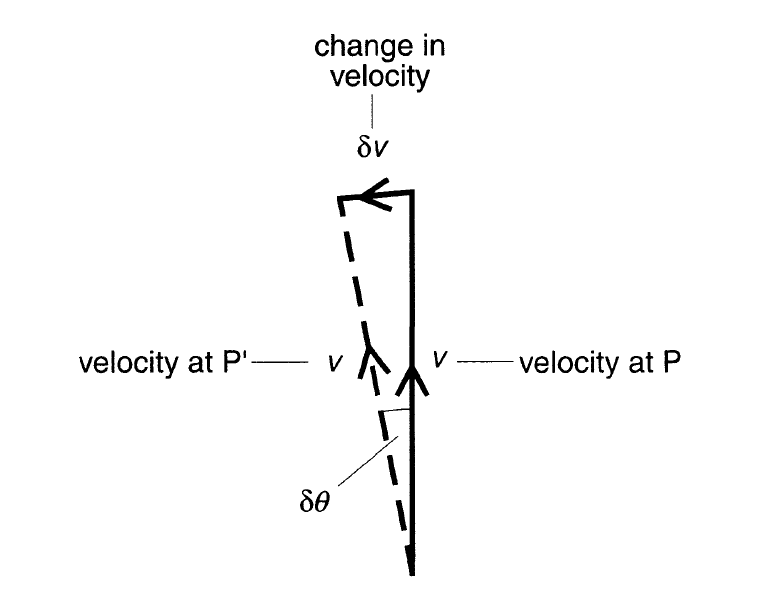
figure 2: velocity at P and P^‘ shown as v which is actually the uniform speed v. At P and P^‘ velocity is different because of different directions at these 2 points.

In figure 2, Velocity at P and P^‘ is shown as v which is actually the uniform speed v at these 2 points. At P and P^‘ velocity is different because of different directions at these 2 points. [Note: When something accelerates, its velocity changes. As velocity is a vector, this can mean a change in speed or direction (or both). Centripetal acceleration is produced by a change in direction, not speed.]

The Δv vector represents the change in velocity because it is the velocity vector that must be added to the velocity at P to produce the new velocity (the resultant) at P’. Here, we will use the concepts of the triangle law of vector addition.

Note that the change in velocity is towards O. In other words, the particle has an acceleration towards the centre of the circle. This is called centripetal acceleration.

If a is the centripetal acceleration, a = δv/δt……….. (1)

But, from the triangle above, δθ = δv/v [ when θ is very small then the value of θ and sine of θ can be taken as same]

So, δv = v δθ ……(2)

From (1) and (2) we get: a = δv/δt = v δθ /δt = vω…… (3)
Using v =ωr, and ω = v/r we get 2 equations of a from equation (3):

a = vω = v. v/r = v² r ………. (4 a)

a = vω = ωr. ω = ω ² r …………. (4 b)

For example, if a particle is moving at a steady speed of 5 m s^-1 in a circle of radius 5 m, its centripetal acceleration a
is found using the middle equation: a= 5²/5 = 5 m s^-2 .

Equations of centripetal acceleration

a = vω = v. v/r = v² r

a = vω = ωr. ω = ω ² r