Normal Force – for horizontal surface and inclined plane with formula
The contact force provided by a surface that is perpendicular to another surface is called the normal reaction force. It is often abbreviated to the normal force and represented by FN or N.
When an object is allowed to fall under the influence of gravity, we can easily see the effect of the force due to gravity. The force due to the gravity of the Earth acts on the object, so the net unbalanced force on it is equal to the force due to gravity, and therefore that object accelerates at –9.80 m/s2. (figure 1)
Normal Force for a Horizontal surface
When the object (say a bin) is at rest on a horizontal surface like a table, as shown in Figure 2, the force due to gravity (Fg = mg) is still acting between the Earth and the bin.
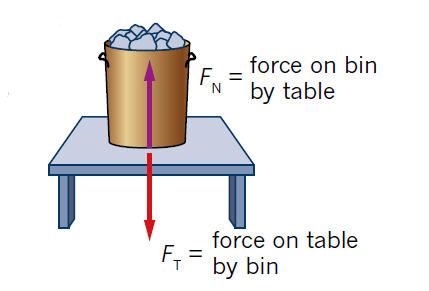
Action–reaction contact forces between the bin and the table.
Since the bin is at rest, there must be another force acting to balance the force due to gravity on the bin. This upwards force is provided by the table.
Because gravity pulls down on the mass of the bin, the bottom of the bin will push down on the surface of the table(downward force – shown by the red arrow in figure 2) and the table provides a reaction force on the bin that is equal and opposite, so it will push upwards on the bin as shown by the purple arrow in figure 2.
The magnitude and direction of the gravitational force on the bin by Earth(downward) are equivalent to the magnitude and direction of the downward force on the table by the bin. Therefore the gravitational force on the bin by Earth is balanced by the upwards contact reaction force on the bin by the table.
Equation of Normal force on a horizontal surface:
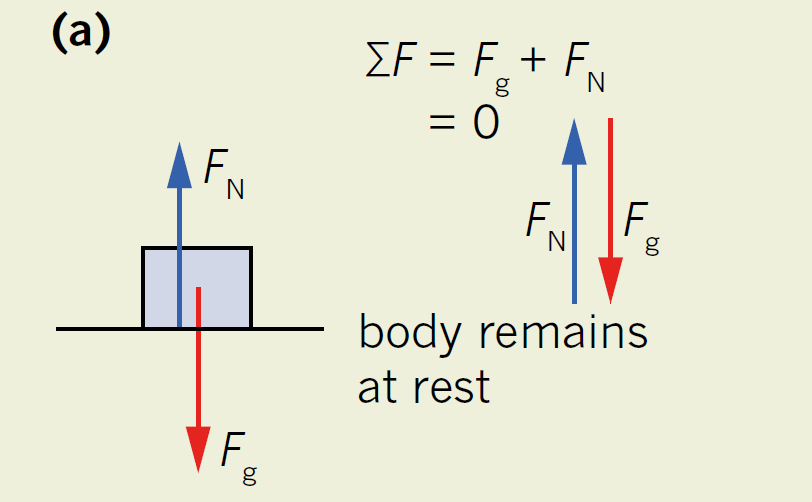
The downward gravitational force on the bin by Earth (Fg) = the downward force on the table by the bin (FT)
Fg = FT …………. (i) [ see figure 2]
& The upwards contact reaction force on the bin by the table (FN) = – the downward force on the table by the bin (Fg)
Equation of Normal force on a horizontal surface: FN = – Fg ……………. (ii) [ see figure 3a]
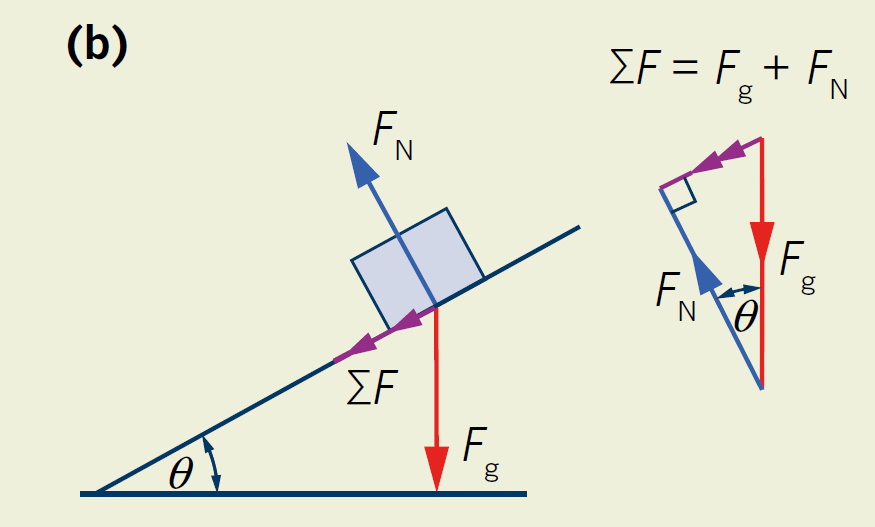
The normal force on an inclined plane
In the example given above the table’s surface is horizontal.
It is possible that an object could be placed on a surface that is tilted so that it makes an angle, θ, to the horizontal.
In this case, the weight force remains the same: Fg = mg downwards.
However, the normal force continues to act at right angles to the surface and will change in magnitude, getting smaller as the angle increases.
The magnitude of the normal force is equal in size but opposite in direction to the component of the weight force that acts at right angles to the surface. So, the normal force is FN = mg cos θ.
The component of the weight force that acts parallel to the surface will cause the mass to slide down the incline. The motion of the object along the plane will be affected by friction if it is present.
The component of the weight force that acts along the surface is given by F = mg sin θ.
Equation of Normal force on an inclined plane:
Equation of Normal force on an inclined plane: FN = mg cos θ
Summary
(a) Where the surface is perpendicular to the force due to gravity, the normal force acts directly upwards.
(b) On an inclined plane, FN is at an angle to Fg and is given by FN = mg cos θ. If no friction acts, the force that causes the object to accelerate down the plane is F = mg sin θ.

