How to Determine g in laboratory | Value of acceleration due to gravity – determination in Lab
Last updated on April 12th, 2021 at 12:02 pm
We will see here how to determine g in the laboratory. g is the symbol of acceleration due to gravity. The basic idea behind determining g in the laboratory is to drop a ball over a known distance and record the time of its descent. The challenge is that the descent happens very quickly.
The methods for measuring g discussed here are (i) Electromagnet and trapdoor method & (ii) Using Lightgates.
Determine the value of g with Electromagnet and trapdoor
Here an electromagnet is used to hold a small steel ball above a trapdoor. The height of the fall h is measured with the ruler as shown in the figure.
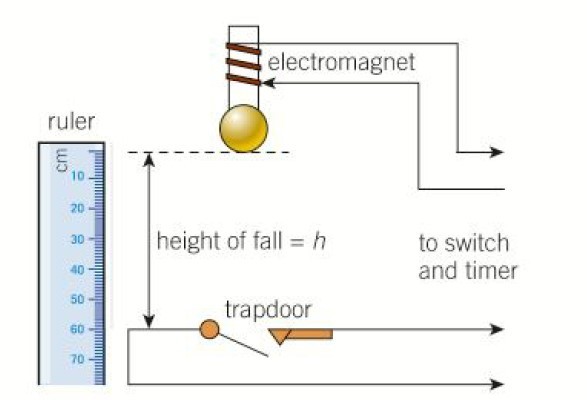
The current is switched off. This results in a few incidents.
1) A timer is triggered as soon as the current is switched off.
2) The electromagnet demagnetizes and
3) the ball falls.
When the ball hits the trapdoor, the electrical contact is broken and the timer stops. Timer value t is noted.
Calculation:The value for g is calculated from the height of the fall(h) and the time taken (t) data using the following motion equation:
h= (½) g t2 …..(i)
=> g =(2 h) /t2
Inaccuracy: Inaccuracy in this experiment is caused by (i) the presence of air resistance and (ii) the slight delay in the release of the steel ball because the magnet takes some time to demagnetize.
Improvement of accuracy: The accuracy of this procedure may be improved by (i) using a heavier ball and (ii) a much longer drop.
Determine the value of g with Light Gates
The electromagnet and trapdoor operation comes with some time delay. So instead of these, we can use Light Gates to determine g. To go for the Light gates method we also need to have two light beams, one above the other, with detectors connected to a timer. The height or distance between the two beams is measured and recorded (h).
– When the ball falls through the first beam, it interrupts the light, and the timer starts.
– When the ball falls through the second beam a known distance further down(h), the timer stops.
– The timer value t is noted.
– Calculation: Now using equation g =(2 h) /t2 we can determine the value of g.
Sample Numerical problem | Solved example for electromagnet & trapdoor procedure to find g
1 ) A ball drops 98.44 cm from an electromagnet to a trapdoor in 0.451 s. Determine the value of g.
Solution:
h = 98.44 cm = 0.9844 m
t = 0.451 s
g =(2 h) /t2 = (2 x 0.9844)/0.4512 = 9.68 m/s2

