Derive formulas of centripetal force & centripetal acceleration
Last updated on May 31st, 2022 at 12:39 pm
In this post, we will derive formulas of centripetal acceleration & centripetal force while we discuss the uniform circular motion.
Uniform circular motion & its acceleration
An object moving with uniform circular motion moves along a circular path of fixed radius at a constant speed. Since the direction of motion of the object is constantly changing, its velocity is also constantly changing.
Therefore, the object in uniform circular motion must be continuously accelerating.
Figure 1 shows an object moving around a circle at a constant speed.
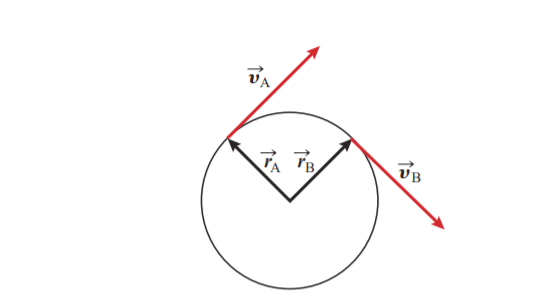
The velocity at point A is vA, and the velocity at point B is vB. The velocities have exactly the same magnitude, v.
The position vector at point A is rA, and the position vector at point B is rB. Both position vectors have magnitude r, as measured from the center of the circle.
At every point on the circle, the velocity of the object is tangential to the circle and perpendicular to the position vector.
The average acceleration is defined as:
aavg = Δv/Δt
Therefore, the direction of average acceleration is parallel to Δv.
Direction of Δv
To determine the direction of Δv, we redraw the position and velocity vectors using the principle that a vector can be translated as long as its magnitude and direction do not change. First, we construct a triangle formed by the two position vectors and the change in position, Δr, as shown in Figure 2. We then construct a triangle formed by the two velocity vectors and the change in velocity.
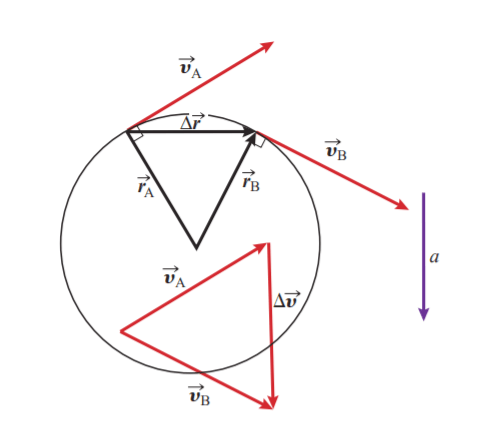
Since the velocity vector is perpendicular to the position vector at either location, we can conclude that the angle subtended by the two-position vectors is equal to the angle subtended by the two corresponding velocity vectors. Further, the two velocity vectors are the same length, as are the two-position vectors; the two triangles from Figure 2 are therefore similar triangles.
We can also see that Δv and, consequently, the average acceleration vector are perpendicular to Δr.
Deriving formula of centripetal acceleration (using differential calculus)
Here, we will derive the formula of centripetal acceleration using differential calculus. If you want to derive this equation using trigonometry only (without using calculus), then you must visit this page that guides you to derive the equation of centripetal acceleration using trigonometry only.
In Figure 3, we repeat the construction for a shorter interval of time between the two points.
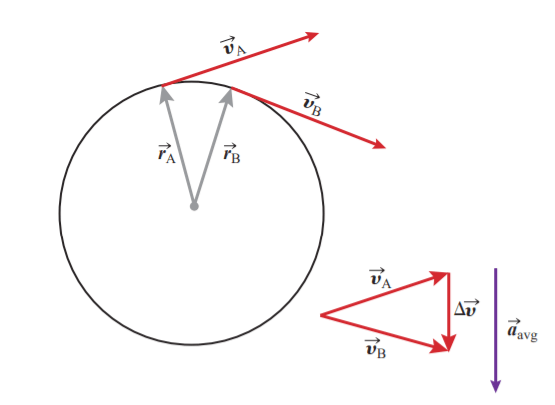
We can see that the conclusions we drew from our construction in Figure 2 still hold.
Next, we take the limit of the average acceleration as Δt goes to zero to get the instantaneous acceleration:
a = limΔt->0 (Δv/Δt) = dv/dt
As the time interval Δt shrinks, so does the displacement between A and B. In the limit, the two points merge. As the position triangle collapses, so does the velocity triangle.
However, the acceleration, which is parallel to Δv, remains perpendicular to Δr, which is a chord of the circle.
The acceleration vector, being perpendicular to that chord, points along the radius to the centre of the circle.
In the limit as Δt goes to zero, the instantaneous acceleration points along the radius. Therefore, an object moving in a circle must continuously accelerate toward the centre of the circle. The acceleration toward the centre of the circle is called radial or centripetal acceleration.
To find the magnitude of the centripetal acceleration, consider the ratios of the two similar triangles formed by the position and velocity vectors:
Δv/v = Δr/r
Δv = v (Δr/r)
Dividing both sides by Δt (the change in time) gives
Δv / Δt = (v Δr)/(r Δt)
In the limit as Δt goes to zero
dv/dt = (v/r) limΔt->0 (Δr/Δt) = (v/r) v …………… (1)
The left-hand side of Equation 1 is the acceleration, so ar = v2/r. This is the equation of centripetal acceleration.
The subscript r on the acceleration denotes that this is the radial acceleration.
We have thus established both the direction and the magnitude for the radial centripetal acceleration of an object moving around a circle at a constant speed.
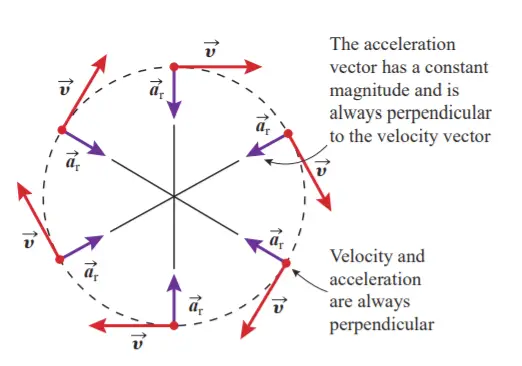
Figure 4 shows the position, velocity, and acceleration vectors for an object executing uniform circular motion. The velocity vector is always tangential to the circle.
The acceleration or centripetal acceleration vector is perpendicular to the velocity vector and points radially inward toward the centre of the circle. The magnitude of the centripetal acceleration vector at any point is the same: ar = v2/r
Deriving formula of centripetal force
We have already derived the equation of centripetal acceleration. Now, we will derive the equation or formula of the centripetal force, using Newton’s second law of motion.
As we know Force F = mass x acceleration,
Hence, centripetal force = mass x centripetal acceleration = m v2/r
The direction of the centripetal force is along the direction of centripetal acceleration, i.e. radially inward toward the centre of the circle.
Related:
derive the equation of centripetal acceleration using trigonometry only
