Polar form and Cartesian form of Vector representation

Last updated on August 2nd, 2021 at 11:27 am

Here we will discuss the Polar form and Cartesian form of Vector representation. Vectors may be represented in two ways: Polar form and Cartesian form. Let’s discuss these in detail.

Polar Form of Vector

In Polar form, a vector A is represented as A = (r, θ) where r is the magnitude and θ is the angle as shown in figure 1.

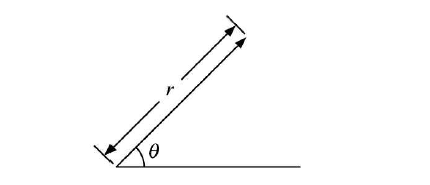
vector resolving using the polar form

Now let’s see how vector resolving is shown using the polar form. Let’s say, a vector R is resolved along X-axis and Y-axis. (2 dimensional). R_x and R_y are the resolved components along the X and Y-axis respectively. As shown in figure2, these two components are represented as follows:

R_x= R cosθ
R_y= R sinθ

These are also known as rectangular components of a vector.

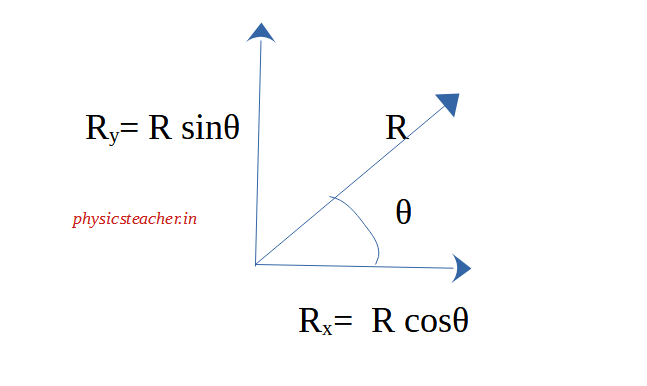
Cartesian form of Vector

In Cartesian form, a vector A is represented as A = A_x i + A_y j + A_z k
Here, A_x, A_y, and A_z are the coefficients(magnitudes of the vector A along axes after resolution), and i, j, and k are the unit vectors along the X-axis, Y-axis, and Z-axis respectively. For example, A_x is the magnitude of vector A resolved along the X-axis.

For simplification, let’s take the same vector R discussed under the Polar form of a vector, and let’s also consider a 2-D system (only X and Y-axis).

Following Cartesian form, R= R_x i + R_y j

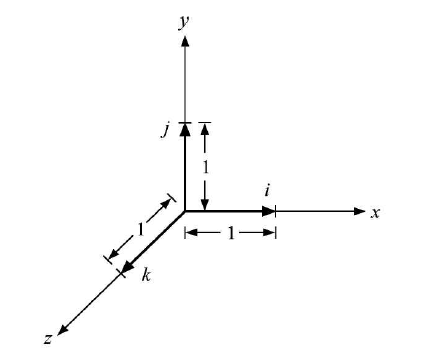
Mixing Polar & Cartesian

From the previous 2 sections,

Following Cartesian form, R= R_x i + R_y j

And, following Polar form,
R_x= R cosθ
R_y= R sinθ

So if we mix these 2 forms, we get: R= R cosθ i + R sinθ j

Numerical solved – Polar to Cartesian conversion

1 ) Convert this vector presentation (10, 30°) of vector R to its cartesian form.

solution:
If in polar form, R = (10, 30°)
To find out the cartesian form, we need to use the resolved or rectangular components of a vector.

then in cartesian form, R = 10 cos30 i + 10 sin30 j
=> R = 8.66 i + 5 j

Numerical solved – Cartesian to Polar conversion

1 ) Convert this vector presentation R = 4 i + 3 j to its polar form.

Solution

We will use the Pythagoras theorem to get the polar form’s magnitude part.

|R| =√(4² + 3²) = 5

And, θ = tan^-1 (3/5) = 31°