Vector Product
Last updated on July 5th, 2023 at 04:03 am
The vector product of two vectors A and B, also called the cross product, is denoted by A X B, and the magnitude of the vector product is found using the formula AB sinφ. Here, A and B are magnitudes of vectors A and B respectively and φ is the angle between the two vectors. The direction of the vector product is found out using the right-hand rule.
As the name suggests, the vector product is itself a vector. We use this vector product to describe torque and angular momentum; We also use it to describe magnetic fields and forces.
Vector Product – definition
We define the vector product of 2 vectors A and B to be a vector quantity with a direction perpendicular to this plane (that is, perpendicular to both vectors A and B) and a magnitude equal to AB sinφ.
That is, if C = AxB, then C= AB sinφ ……………….. (equation 1)
[ Here, A and B are magnitudes of vectors A and B respectively. φ is the angle between A and B.
C is the magnitude of the vector C.
And, C= (cross) product of A and B]
Also read: Scalar Product
Examples of Vector Product
We use this vector product to describe torque and angular momentum; We also use it to describe magnetic fields and forces.
Vector Product – Calculation process | How to determine a vector product
To define the vector product A X B, we draw the two vectors A and B with their tails at the same point (Fig. 1(a)). The two vectors then lie in a plane.
We measure the angle φ from A toward B and take it to be the smaller of the two possible angles, so φ ranges from 0° to 180° Then sin φ≥ 0 and C in Eq. (1) is never negative, as must be the case for a vector magnitude.
Note also that when A and B are parallel or antiparallel, φ= 0 or 180° and C = 0. That is, the vector product of two parallel or antiparallel vectors is always zero. In particular, the vector product of any vector with itself is zero.
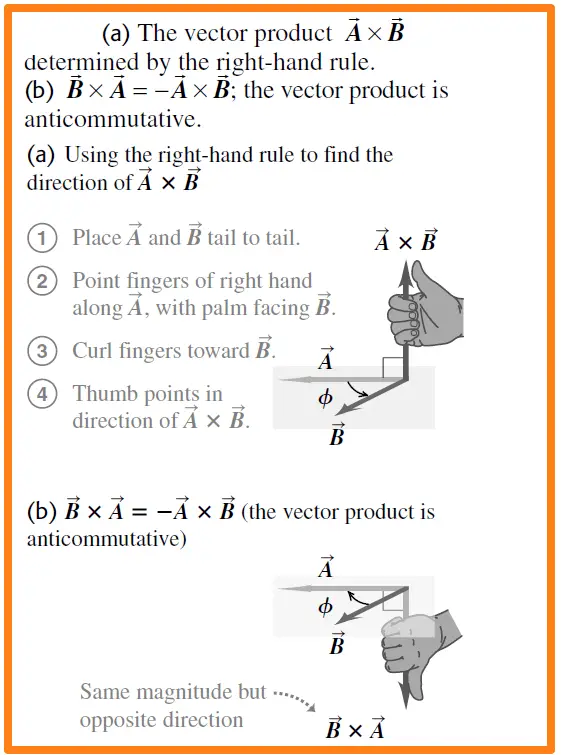
The direction of the vector product using the right-hand rule
There are always two directions perpendicular to a given plane, one on each side of the plane. We choose which of these is the direction of A× B. We need to adopt the right-hand rule and follow the steps to determine that direction.
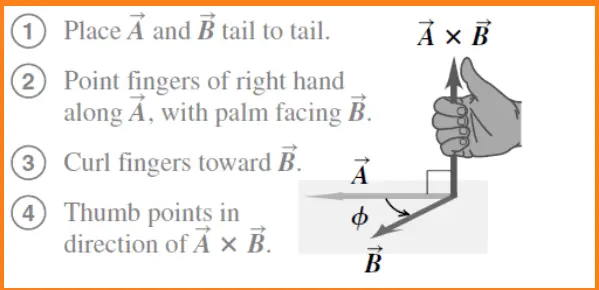
Finding out the direction of the vector product using the right-hand rule
- Place vectors A and B tail to tail.
- To find out A× B, point the fingers of the right hand along vector A, with the palm facing vector B.
- Curl fingers toward B
- The thumb of the right-hand points to the direction of A x B.
Similarly, we determine the direction of B× A by rotating B into A as in Fig. 1b. The result is a vector that is opposite to the vector A× B. The vector product is not commutative!
In fact, for any two vectors A and B, A× B = −B × A ………………. (equation 2)
The magnitude of a Vector Product is never zero
We measure the angle φ from A toward B and take it to be the smaller of the two possible angles, so φ ranges from 0° to 180° Then sin φ≥ 0 and C in Eq. (1) is never negative, as must be the case for a vector magnitude.
Vector Product of 2 parallel or antiparallel vectors is always zero
Note also that when A and B are parallel or antiparallel, φ= 0 or 180° and C = 0. That is, the vector product of two parallel or antiparallel vectors is always zero. In particular, the vector product of any vector with itself is zero.
The vector product of any vector with itself is zero – how?
As we go to get the vector product of any vector with itself, we get φ= 0. And, sinφ = sin 0 degree = 0. As a result, the result AB sinφ becomes 0.
Calculating the Vector Product Using i,j,k unit vectors
If we know the components of A and B, we can calculate the components of the vector product using a procedure similar to that for the scalar product. First, we work out the multiplication table for the unit vectors î, ĵ, kˆ, and, all three of which are perpendicular to each other (Fig. 3).
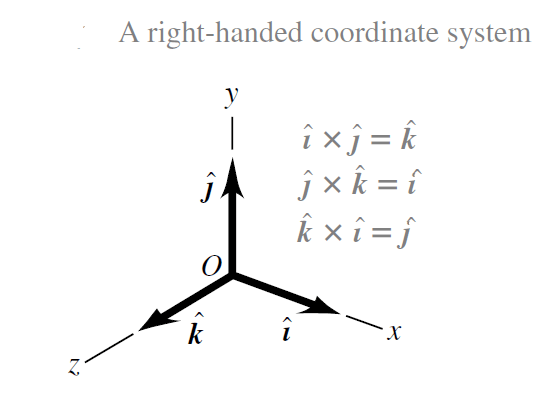
The vector product of any vector with itself is zero, so,


Also read: Vector Physics
