Using the Vector Cross product to find the Area of a Triangle

Let’s see how to use the Vector Cross product to find the Area of a Triangle. Here we will see that half of the magnitude of the cross product of vector AB and AC gives the area of the triangle ABC. (reference: the image below)

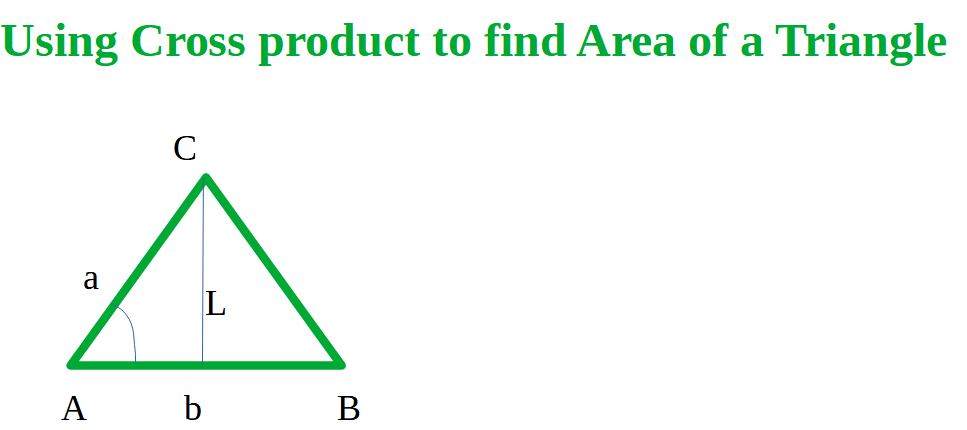
Let, AB and AC are 2 vectors and these are taken as 2 adjacent sides of triangle ABC. The magnitude of AB and AC are b and a respectively, which are the length of two sides of the triangle as well.

L is the height of the triangle and θ is the angle CAB.
Hence, L = a sin θ

Area of ABC = (½) AB . L = (½) b a sin θ ………… (1)
And, |AB x AC| = b a sin θ …………… (2)

So, Area of ABC = (½) |AB x AC|

Here we can see that half of the magnitude of the cross product of vector AB and AC gives the area of the triangle ABC.