Parallelogram Law of Vector Addition

State Parallelogram Law of vector addition

If a parallelogram can be drawn so that two vectors can be placed with their tails connected as the two adjacent sides of the parallelogram with an angle θ between them, then the diagonal of the parallelogram represents their resultant vector or the vector sum.

Derive the formulas of the resultant vector using the Parallelogram Law of vector addition

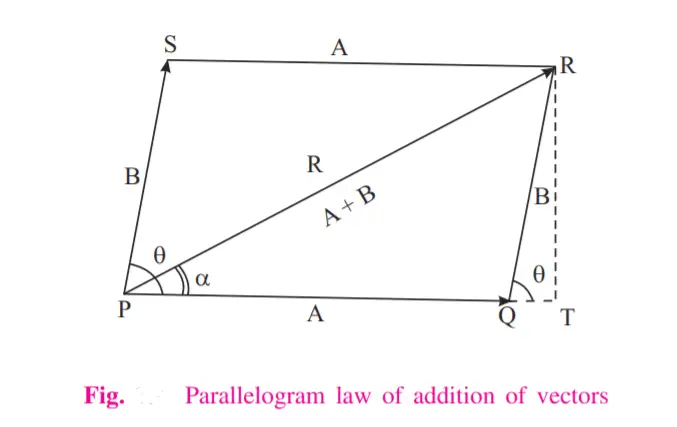
Let A and B be the two vectors and let θ be the angle between them as shown in Fig. above. To calculate the vector sum, we complete the parallelogram.

Here side PQ represents vector A, side PS represents B and the diagonal PR represents the resultant vector R. Here, α angle is the angle the resultant makes with the base vector and the angle denotes the direction of the resultant or the vector sum.

Sample Numerical to find the sum of 2 force vectors using the Parallelogram Law

Force A has a magnitude of 30 N and it makes an angle of 30 degrees with another force B of magnitude 40 N. What is the vector sum or resultant of forces A and B?

Solution:

Let, R be the vector sum of forces A and B.

|R| = √[30² + 40² + 2.30.40 cos 30] = 67.66 N

If resultant force R makes an angle α with A then tan α = (B sinθ)/(A + Bcosθ)
here, A = 30, B = 40, θ = 30.

tanα = 40 sin 30 / (30 + 40 cos 30) = 20/(30 + 34.64) = .31

α = arctan (.31) = 17.22 degree

Answer: The resultant force is 67.66 N at 17.22 degrees from force A