Vector Subtraction

Last updated on April 16th, 2021 at 10:04 am

As we have discussed Vector in physics and had a detailed study of Vector addition, now its turn to discuss another topic of vector physics which is Vector Subtraction.

Vector Subtraction helps us to subtract one vector from another vector. Now how do it?

To subtract one vector from another, for example, to get A – B, simply form the vector –B, which is the scalar multiple (–1)B, and add it to A i.e.
A – B = A + (–B)

Vector – subtracting with examples

Example: For the two vectors A and B in the diagram 1, find the vector A– B.

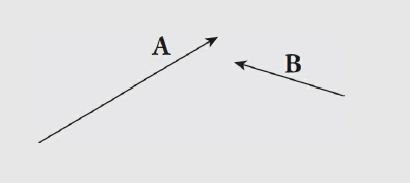
Solution. Flip B around i.e. reverse the direction of B (thereby forming –B) and add that vector to A using triangle law of vector addition.

Here is another example. The diagram 3 below shows 2 vectors A and B and how A-B is derived.

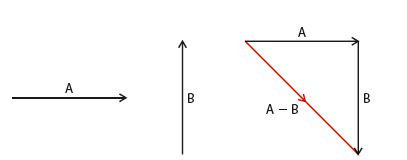
Vector subtraction – one Use case

Now let’s discuss one use case of vector subtraction where we need to subtract a vector from another vector. If you are aware of the term ‘relative velocity’, probably you have already got a hint.

When we discuss the motion of different objects situated near the earth’s surface, we take earth surface as the ‘static’ frame of reference. An object is said to be in motion with respect to a viewer on this static frame of reference.
That’s cool.

But if we have to consider the motion of an object with respect to a ‘moving frame of reference’, then how to handle that situation?

For example, to a passenger in a running train, all nearby houses, trees, and other static objects seem to be in motion. That means with respect to that passenger in a running train those objects have a ‘relative velocity’, though they are actually motionless or static.

Relative velocity calculation – When we have to calculate the relative velocity of an object with respect to a viewer in motion, we have to subtract the actual velocity of the viewer from the actual velocity of the object.

Say the actual velocity of the object is V1 and the actual velocity of the viewer is V2.
Then the relative velocity of the object with respect to the viewer in motion =Vr = V1 – V2

Now while calculating the difference between V1 and V2, we will use the vector addition process but with a tweak.

It’s here: V1-V2 = V1 + (-V2)

So we have to consider the negative of the V2 vector, which means a vector with the same magnitude as V2 but with reverse direction.

And then follow the known vector addition process between V1 and (-V2) and get the vector V1-V2.

Numericals Problems – vector subtraction

1)
A car is moving with a velocity of 80 km/hr towards north. A bus is moving with a velocity of 80√2 km/hr towards north-west. What is the relative velocity of the bus with respect to the car?

2)
One ship is moving towards east with a velocity of 10 kmph. A boat is moving towards north-east, making an angle 30 degree with north. If to a viewer on the ship the boat seems to move towards north, then what is the velocity (magnitude) of the boat?

Relative Velocity of rain with respect to a moving observer

With the help of vector subtraction mechanism we just discussed, we can easily find out the relative velocity of rain with respect to a moving observer.

If there is not any considerable wind flow then rain drops come down vertically.

Now a person at rest can hold the umbrella vertically above his head and can escape the raindrops.
But if the person himself is in motion then he has to hold the umbrella in a slanted position pointing towards his front side to save from rain.

We can take help of vector diagram and vector subtraction procedure to discuss this.

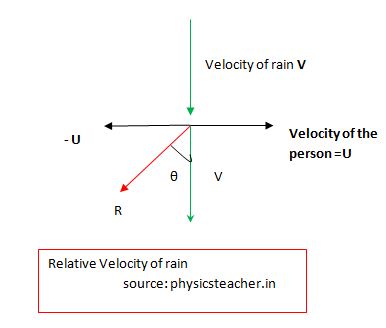
Say, the vertically downward velocity of raindrops is V and the person is moving towards east with a velocity U.

Now say, with respect to the moving observer (the person) the relative velocity of the raindrops is R.

So we will get R by subtracting observer’s velocity from the rain velocity.
R = V – U = V + (-U)

In the diagram, a reverse vector of U is drawn by flipping U and is shown as –U.

Remember that this flipped vector has same magnitude as that of the original U but the – sign only shows a reverse direction.

In the following calculation, we will use its magnitude only, as we can take it as a new vector.

Now if we add these 2 vectors V and –U using Vector addition (Here Pythagoras theorem is a better option to do this addition as the 2 vectors V and –U are at right angle), we get R, the relative velocity of rain.

Magnitude of R = √(V² + U²) ……………….(1)

And also we get the angle θ it makes with vertical line, from the equation below:
tan θ  = U/V …………….(2)

As we note that R makes an angle θ with vertical, so it’s evident that the raindrops seem to come in a slanted path from the front side of the person in motion.