Using Vector Cross product to find Area of a Parallelogram

Let’s see how to use the Vector Cross product to find the Area of a Parallelogram. Here we will see that the magnitude of the cross product of vector AB and AC gives the area of the parallelogram ABCD. (reference: the image below)

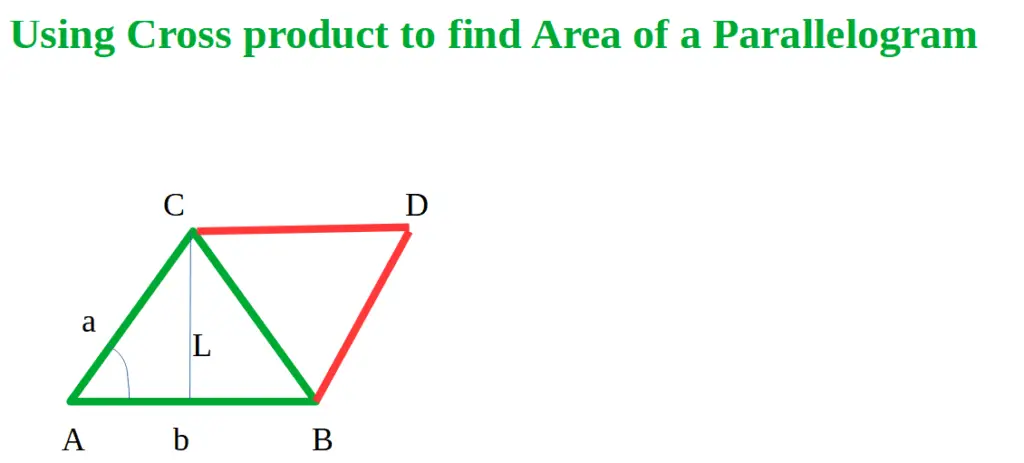
ABCD is a parallelogram and its area is twice the area of the ABC triangle.

As Area of ABC triangle = (½) | AB x AC |, (see the proof: here) hence we can represent the area of ABCD as per the following way:

Area of ABCD = 2 . Area of ABC = 2. (½) | AB x AC| = | AB x AC|

Here we can see that the magnitude of the cross product of vector AB and AC gives the area of the parallelogram ABCD.