Vectors class 11 Physics revision notes – chapter 4

Last updated on July 5th, 2023 at 08:49 pm

This post covers Vectors class 11 Physics revision notes – chapter 4 with concepts, formulas, applications, numerical, and Questions. These revision notes are good for CBSE, ISC, UPSC, and other exams. This covers the grade 12 Vector Physics syllabus of some international boards as well. Here we have covered Vector fundamentals & types, Laws for vector addition, dot and cross products, & relative velocity of rain with respect to a moving man (with numerical).

There are physical quantities that require both magnitude and direction for their complete description. A simple example of a vector is velocity. The statement that the velocity of a train is 100 Km/hour does not make much sense unless we also tell the direction in which the train is moving.

Force is another such quantity. We must specify not only the magnitude of the force but also the direction in which the force is applied. Such quantities are called vectors. A vector quantity has both magnitude and direction. Some examples of vector quantities in mechanics are displacement, acceleration, momentum, angular momentum, torque, etc.

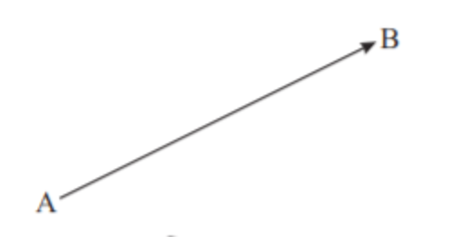
A vector is represented by a line with an arrow indicating its direction. Take vector AB in Fig. 1. The length of the line represents its magnitude on some scale. The arrow indicates its direction.

[ All our posts on Vector are clubbed here: Vector Physics tutorials. Read these for a better understanding ]

---

Types of Vectors class 11

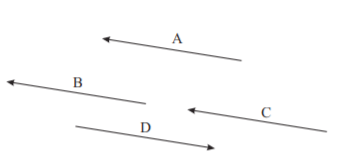
Equal Vector

Two vectors are said to be equal if their magnitudes are equal and they point in the same direction.
Three vectors A, B, and C shown in the Figure are equal.
We say A = B = C.
But D is not equal to A.

Negative of a Vector

A vector (here D in the figure above) that has the same magnitude as A but has opposite direction, is called negative of A, or –A. Thus, D = –A

Null Vector or Zero Vector

A vector is said to be a zero or null vector if the magnitude of the vector is zero, i.e., the starting point and the endpoint of the Vector are the same.

Unit Vector class 11

A vector is said to be a Unit vector if its magnitude is 1 unit and it has a specified direction. A unit vector is a dimensionless vector having a magnitude of exactly 1. Unit vectors are used to specify a given direction and have no other physical significance. They are used solely as a convenience in describing a direction in space.

It has neither units nor dimensions.

As an example, we can write vector A as A n where a cap(^) on n denotes a unit vector in the direction of A. A unit vector has been introduced to take care of the direction of the vector; the magnitude has been taken care of by A.

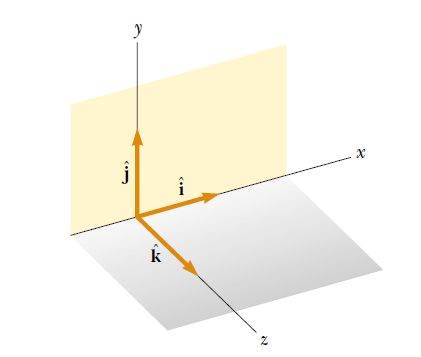
The unit vectors along coordinate axes are of particular importance. We shall use the symbols i, j, and k to represent unit vectors pointing in the positive x, y, and z directions, respectively. The “^ hats” on the symbols are a standard notation for unit vectors, but many times just a bold font(like i) is popularly used without using the hat.

The unit vectors i, j, and k form a set of mutually perpendicular vectors in a right-handed coordinate system, as shown in Figure. The magnitude of each unit vector equals 1;
that is, | i | = | j | = | k | = 1.

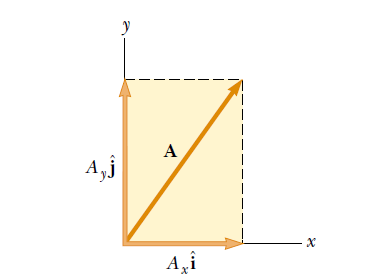
The unit vector along the x-axis is denoted by i, along the y-axis by j, and along the z-axis by k.

Using this notation, vector A, whose components along the x and y axes are respectively A_x and A_y, can be written as A = A_x i + A _y j

Addition of Vectors class 11

Vectors of the same kind only can be added. For example, two forces can be added or two velocities can be added. But a force and a velocity cannot be added. Here we will discuss the Triangle Law and the Parallelogram Law to add vectors.

Triangle Law of Vector Addition class 11

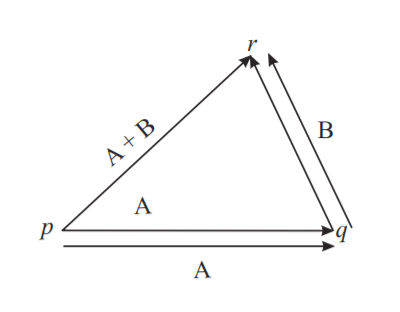
If two vectors are represented in magnitude and direction by the two sides of a triangle taken in order, the resultant is represented by the third side of the triangle taken in the opposite order. This is called the triangle law of vectors.

The sum of two or more vectors is called the resultant vector. In Fig. above, pr is the resultant of A and B

Parallelogram Law of Vector Addition class 11

If a parallelogram can be drawn so that two vectors can be placed with their tails connected as the two adjacent sides of the parallelogram with an angle θ between them, then the diagonal of the parallelogram represents their resultant vector or the vector sum.

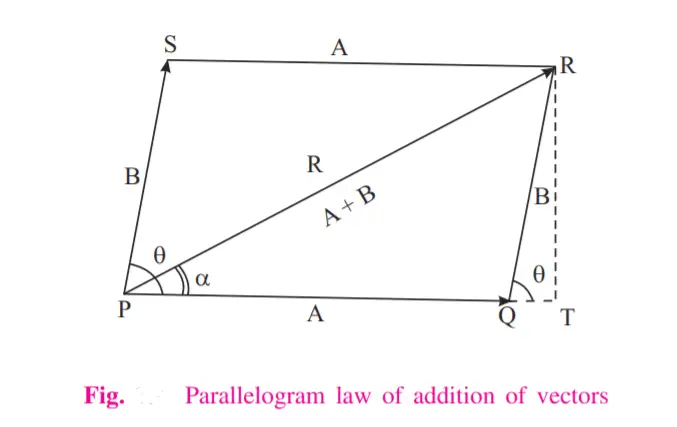
Let A and B be the two vectors and let θ be the angle between them as shown in Fig. above. To calculate the vector sum, we complete the parallelogram. Here side PQ represents vector A, side PS represents B and the diagonal PR represents the resultant vector R. Here,α angle is the angle the resultant makes with the base vector and the angle denotes the direction of the resultant or the vector sum.

Resultant vector formulas (Magnitude and direction)

Vector Numerical problems class 11 (solve using Parallelogram Law & Triangle Law)

1)

Vector A has a magnitude of 30 and it lies in such a way that it makes an angle of 30 degrees with another vector B of magnitude 40. What is the vector sum or resultant of A and B?

Solution: Let, R be the vector sum of A and B.

|R| = √[30² + 40² + 2.30.40 cos 30] = 67.66

If R makes an angle α with A then tanα = (B sinθ)/(A + Bcosθ)
here, A = 30, B = 40, θ = 30.

tanα = 40 sin 30 / (30 + 40 cos 30) = 20/(30 + 34.64) = .31

α = arctan (.31) = 17.22 degree

Answer: The resultant is 67.66 at 17.22 degrees from A

2)

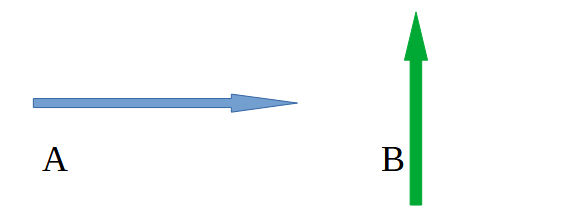
A and B are two forces where |A| = 3 N and |B| = 4 N.

Can you draw the vector sum of these two forces using the triangle law?
Also, find out its magnitude and direction using some suitable formula.

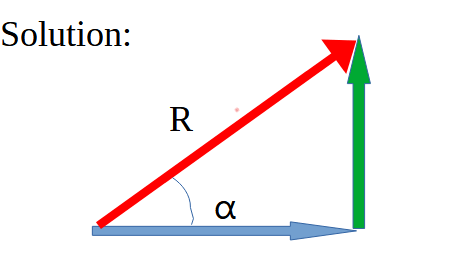
Solution: Using Triangle law, vectors A and B are drawn in the tail to tip way to draw 2 sides of the triangle. R, the 3^rd side of the triangle (in red) shows the vector sum of A and B.

The magnitude of the vector sum can be calculated using the Pythagoras theorem in this case and B is perpendicular to A. So the magnitude of the vector sum: |R| = √(3² + 4²) = 5 N

If it makes an angle α with A, then tanα = 4/3

α = arctan (4/3) = 53.13

So, the vector sum is 5 N at 53.13 degrees from A

The next section covers the Multiplication of vectors – dot and cross, formulas, rules, and numerical problems.

Product of vectors class 11

Dot product

The scalar multiplication of two vectors yields a scalar product. Scalar multiplication is also known as the dot product.

The formula of Dot Product

The scalar product or dot product of 2 vectors A and B is expressed by the following equation:
A.B = AB cos φ, where φ is the angle between the vectors, A is the magnitude of vector A and B is the magnitude of vector B.
The scalar product is also called the dot product because of the dot notation that indicates it.

Rules of Dot product or Scalar product

1) Dot product is a scalar, it is commutative: A.B = B.A = ABcosθ.
2) It is also distributive: A.(B + C) = A.B + A.C.

3)

i . j = j . i = 0
j . k =k . j =0
k . i =i . k =0

i . i = 1
j . j = 1
k . k = 1

4)
If, A = (A_x i + A_y j + A_z k) and B = (B_x i + B_y j + B_z k)
Then find A.B

A . B = (A_x i + A_y j + A_z k) . (B_x i + B_y j + B_z k)
= (A_x i . B_x i + A_x i . B_y j + A_x i . B_z k)
+ (A_y j . B_x i + A_y j . B_y j + A_y j . B_z k )
+ (A_z k . B_x i + A_z k . B_y j + A_z k . B_z k )

= (A_x B_x i . i + A_x B_y i . j + A_x B_z i . k)
+ (A_y B_x j . i + A_y B_y j . j + A_y B_z j . k )
+ (A_z B_x k . i + A_z B_y k . j + A_z B_z k . k )
= A_x B_x + A_y B_y + A_z B_z

Vector Product

We define the vector product to be a vector quantity with a direction perpendicular to this plane (that is, perpendicular to both A and B) and a magnitude equal to AB sinφ.

Formula of Vector Product or Cross Product

if C =AxB, then C= AB sinφ ……………….. (equation 1)
[ Here, A and B are magnitudes of vectors A and B respectively.
C is the magnitude of the vector C.
And, C= (cross) product of A and B ]

The direction of the product vector C =A × B is given by the right-hand rule. If the right hand is held so that the curling fingers point from A to B through the smaller angle between the two, then the thumb stretched at right angles to fingers will point in the direction of C.

Rules of Vector Product or Cross Product

1) Direction of vector BxAis opposite to that of the vector AxB. This means that the vector product is not commutative.

2)
ix j = k
j x k =i
k x i =j

j x i = – k
k x j = – i
i x k = – j

i x i = 0
j x j = 0
k x k = 0

3) If, A = (A_x i + A_y j + A_z k) and B = (B_x i + B_y j + B_z k)
Then find A X B

A X B = (A_x i + A_y j + A_z k) x (B_x i + B_y j + B_z k)

= (A_x i xB_x i + A_x i x B_y j + A_x i x B_z k)
+ (A_y j x B_x i + A_y j x B_y j + A_y j x B_z k )
+ (A_z k x B_x i + A_z k x B_y j + A_z k x B_z k )

= (A_x B_x i x i + A_x B_y i x j + A_x B_z i x k)
+ (A_y B_x j x i + A_y B_y j x j + A_y B_z j x k )
+ (A_z B_x k x i + A_z B_y k x j + A_z B_z k x k )

= 0 + A_x B_y k + A_x B_z (-j) + A_y B_x (-k) + 0 + A_y B_z i + A_z B_x j + A_z B_y (-i) + 0
= (A_y B_z – A_z B_y ) i + (A_z B_x – A_x B_z) j + (A_x B_y – A_y B_x) k

Vector Numerical Problems class 11 (on Dot Product and Cross Product)

1) Find out the dot product of vector A and B where A = 4i + 5 j + 2k, B = 6i – 4 j + 3k.

Dot product D = A_x B_x + A_y B_y + A_z B_z = 4.6 + 5(-4) + 2.3 = 24 – 20 + 6 = 10

2) Find out the cross product of vector A and B where A = 4i + 5 j + 2k, B = 6i – 4 j + 3k.

Cross Product C = (A_y B_z – A_z B_y ) i + (A_z B_x – A_x B_z) j + (A_x B_y – A_y B_x) k

=(5.3 – 2(-4)) i + (2.6 – 4.3) j + (4(-4)-5.6) k

= 23 i + 0j -46k = 23i – 46k

In the next section, we have discussed and solved numerical problems related to the Relative velocity of Rain with respect to a Moving Man with the help of Vector subtraction.

Relative Velocity of Rain to a Moving Man | Vector Subtraction Numerical class 11

Raindrop and moving man – relative velocity (Problem number 1)

Rain is falling vertically at a speed of 35 m/s. A man rides a bicycle with a speed of 12 m/s in the east-to-west direction. What is the direction in which he should hold his umbrella?

Solution:

Velocity of rain = V_r = 35 m/s

Velocity of man = V_m = 12 m/s east to west

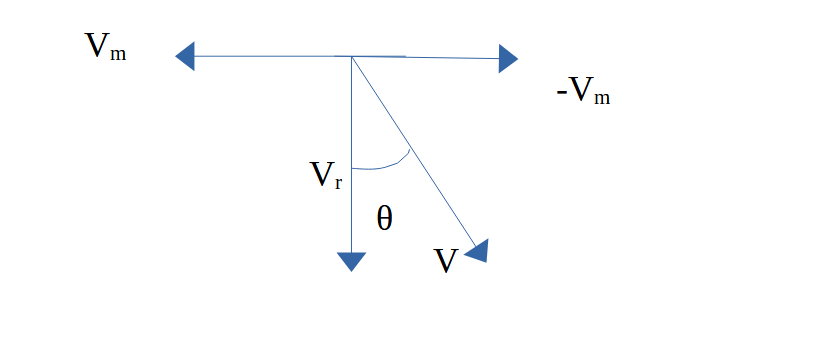
The relative velocity of rain with respect to the man =V = V_r – V_m

=> V = V_r + (– V_m)
In the diagram, we have reversed the direction of the man to draw – V_m

Now, Let this relative velocity V make an angle θ with the vertical.
tan θ = V_m / V_r = 12/35

θ = arctan (12/35) = 18.9 degrees with the vertical towards the west.

The man has to hold his umbrella at 18.9 degrees with the vertical.

Raindrop and moving man – relative velocity (Problem number 2)

Rain is falling vertically at a speed of x m/s. A man rides a bicycle with a speed of 12 m/s in the east-to-west direction. What is the value of x if the direction in which he holds his umbrella is 21 degrees with the vertical?

Solution:

Velocity of rain = V_r = x m/s

Velocity of man = V_m = 12 m/s east to west

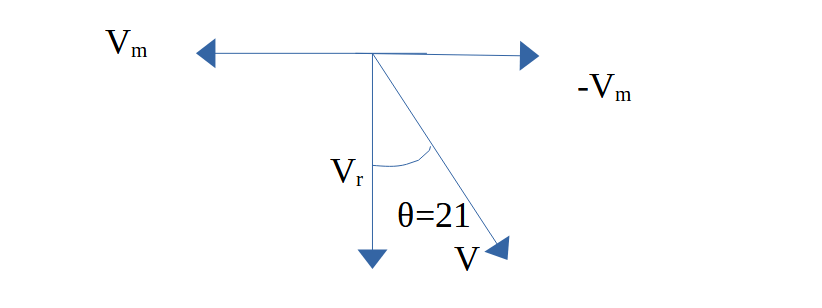
The relative velocity of rain with respect to the man =V = V_r – V_m

=> V= x + (– V_m)

In the diagram, we have reversed the direction of the man to draw – V_m

If this relative velocity V makes an angle θ = 21 degrees with the vertical.
tan 21 = V_m / V_r = 12/x

=> 0.38 =12/x

x=12/0.38=31.57 m/s

Rain is falling vertically with a speed of 31.57 m/s

Raindrop and moving man – relative velocity (Problem number 3)

Rain is falling vertically at a speed of 40 m/s. A man rides a bicycle with a speed of 12 m/s in the east-to-west direction. What will be the magnitude of the relative velocity of rain with respect to the man? (i.e. What would be the apparent velocity of rain to the cyclist?)

Solution:

Velocity of rain = V_r = 40 m/s

Velocity of man = V_m = 12 m/s east to west

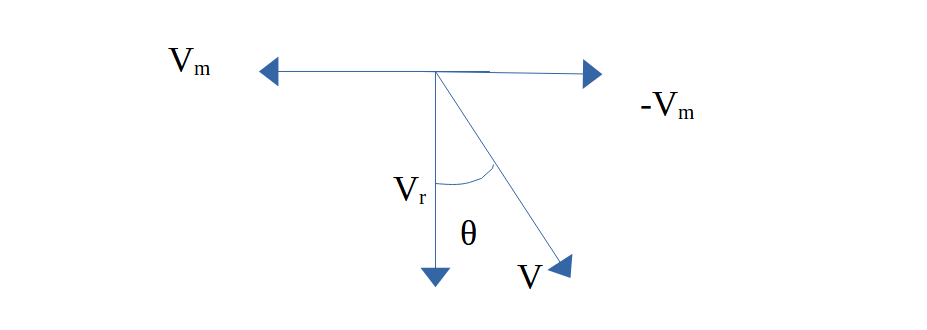
The relative velocity of rain with respect to the man =V = V_r – V_m

=> V= V_r + (– V_m)

In the diagram, we have reversed the direction of the man to draw – V_m

Now V = √( V_r² + V_m²) = √( 40² + 12²) = 41.76 m/s

Hence, the apparent velocity of rain to the cyclist=41.76 m/s

Note: All our posts on Vector are clubbed here: Vector Physics tutorials. Read these for a better understanding