Scalar product formula with an example

Last updated on April 14th, 2021 at 05:17 pm

Scalar multiplication of two vectors yields a scalar product. Scalar multiplication is also known as the dot product. In the next section, we will see how the scalar product formula or equation is written.

Scalar product formula | equation of dot product

The scalar product of 2 vectors A and B is expressed by the following equation:
A.B = AB cos φ, where φ is the angle between the vectors, A is the magnitude of vector A and B is the magnitude of vector B.

The scalar product is also called the dot product because of the dot notation that indicates it.

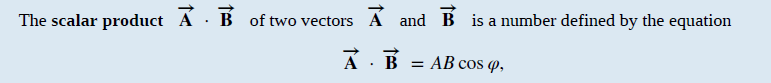
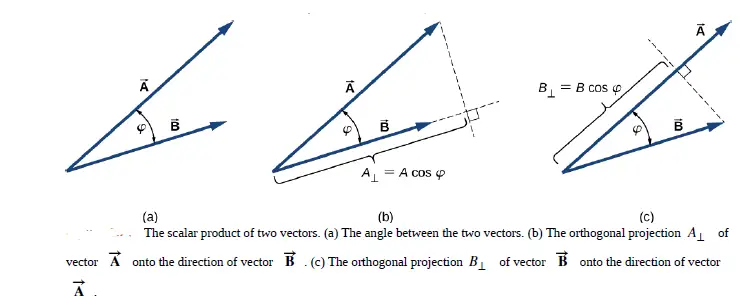
In figure (b), vector A is projected along the direction of vector B, as a result, a projected component of vector A is generated along the direction of vector B. And this component is A cos φ.

Similarly, in figure (c), the vector B is projected along the direction of vector A, as a result, a projected component of vector B is generated along the direction of vector A. And this component is B cos φ.

In both cases, you can see how the cos φ is generated as we are working to find out a scalar product of 2 vectors A and B.

Numerical problem solving using the scalar product or dot product

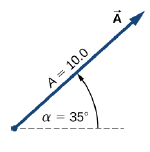
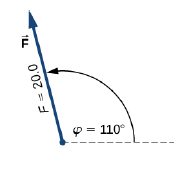
Two vectors A and F are shown in the above 2 diagrams. Find the scalar or dot product of A and F.

Solution

From Figure, the magnitudes of vectors A and F are A = 10.0 and F = 20.0.

Angle θ , between them, is the difference: θ = φ − α = 110° − 35° = 75° .

Substituting these values into Equation of scalar product gives the scalar product.

A straightforward calculation gives us A.F = AF cos θ = (10.0)(20.0) cos 75° = 51.76.

Work is scalar or vector?

Work is a scalar. It’s a scalar product of 2 vectors, force, and displacement. As work is scalar, only the Magnitude of work counts.

Energy is scalar or vector?

Energy is a scalar. only the Magnitude of energy counts.

Power is scalar or vector?

Power is a scalar quantity. It has no direction attached. Magnitude of power only matters.