Magnetic field lines of permanent magnets & current-carrying wires | How to calculate the magnetic field at an arbitrary distance from the wire?
Last updated on October 6th, 2021 at 03:01 pm
Let’s learn the idea of magnetic field lines of permanent magnets & current-carrying wires, how these lines behave in the situation of permanent magnets and current-carrying wires, and also how to calculate the magnetic field at an arbitrary distance from the current-carrying wire. You can quickly revise the Magnetic field and magnetic field line properties here.
Magnetic field of permanent magnets & electron spin
Permanent magnets (like refrigerator magnets) consist of atoms, such as iron, for which the magnetic moments (roughly electron spin) of the electrons are “lined up” all across the atom. This means that their magnetic fields add up, rather than canceling each other out. The net effect is noticeable because so many atoms have lined up.
magnetic field lines of a bar magnet & atomic spin – diagram
The magnetic field lines of a bar magnet always point from the north pole to the south.
The magnetic field of a bar magnet, for example, is illustrated below:
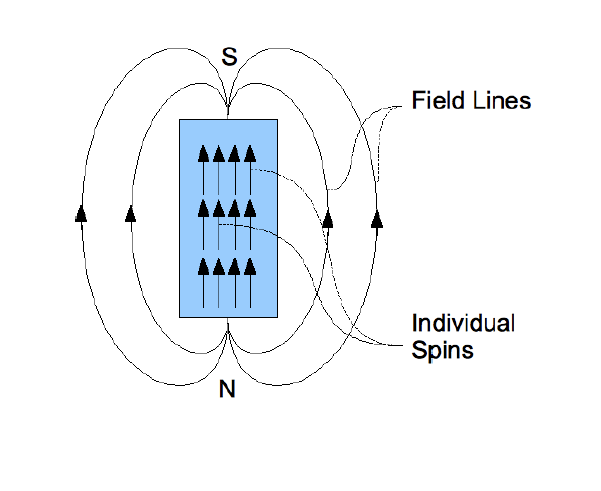
The figure above shows how the magnetic moments (roughly electron spin) of the electrons are “lined up” across the atom.
cutting a bar magnet in half
If we were to cut the bar magnet (shown above) in half, it would still have north and south poles; the resulting magnetic field would be qualitatively the same as the one above (but weaker).
Magnetic field lines generated by current-carrying wires
Here, we will discuss and answer a few common & frequently asked questions on the magnetic fields generated by current-carrying wires.
how to calculate the magnetic field at an arbitrary distance from the current-carrying wire?
Charged particles in motion also generate magnetic fields. The most frequently used example is a current-carrying wire since current is literally moving charged particles.
The magnitude of a field generated by a current-carrying wire depends on the distance to the wire and the strength of the current (I). We use the formula below to calculate the magnetic field at an arbitrary distance from the current-carrying wire.
Magnetic field at a distance r from a current-carrying conductor:
Bwire = (μ0 I)/ (2 π r) where μ0 = permeability of Vacuum = 4π x 10-7 Tm/A
how to find the direction of the magnetic field at an arbitrary distance from the current-carrying wire?
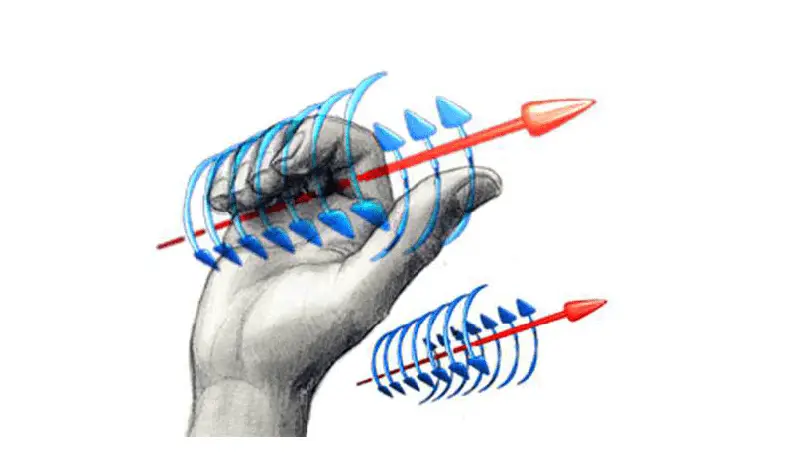
Meanwhile, its direction can be found using the so-called first right-hand rule: point your thumb in the direction of the current. Then, curl your fingers around the wire. The direction your fingers will point in the same direction as the field. Be sure to use your right hand!
Representing 3-dimensional magnetic fields on a Two-dimensional sheet of paper
Sometimes, it is necessary to represent such three-dimensional fields on a two-dimensional sheet of paper. The following example illustrates how this is done.
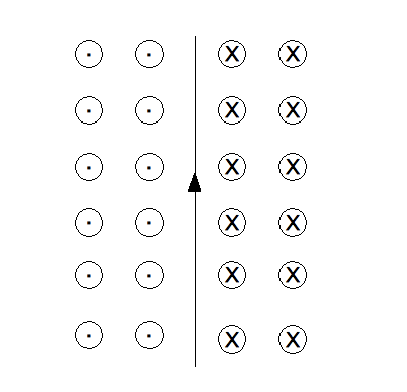
In the example above, a current is running along a wire towards the top of your page (2-Dimensional). The magnetic field is circling the current-carrying wire in loops that are perpendicular to the page.
Where these loops intersect this piece of paper, we use the symbol ‘circle with a dot in its center’ to represent where the magnetic field is coming out of the page and the symbol ‘circle with a cross inside’ to represent where the magnetic field is going into the page. This convention can be used for all vector quantities: fields, forces, velocities, etc.
Also, you may go through an in-depth post on the Motor effect and Generator effect.
Related: Magnetism class notes PDF download
