A block of mass 0.500 kg slides on a flat smooth surface with a speed of 2.80 m/s. It then slides over a rough surface with μk and slows to a halt. While the block is slowing,.. [Friction numerical]
Friction Numerical Problem)
A block of mass 0.500 kg slides on a flat smooth surface with a speed of 2.80 m/s. It then slides over a rough surface with μk and slows to a halt. While the block is slowing,
(a) what is the frictional force on the block?
(b) What is the magnitude of the block’s acceleration?
(c) How far does the block slide on the rough part before it comes to a halt?
Solution:
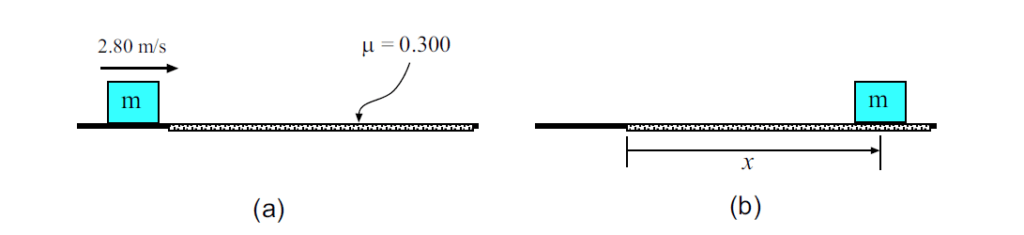
(a) Block is sliding on a smooth surface with a speed of 2.80 m/s. It encounters a surface that is rough, with μk = 0.300.
(b) Block has come to a halt after moving a distance x on the rough surface.
(a)
The problem is illustrated in Fig. 1. As indicated in Fig. 1 the block slides a distance of x before coming to a halt on the rough surface.
First, let’s find the forces which act on the block by drawing Fig. 2.
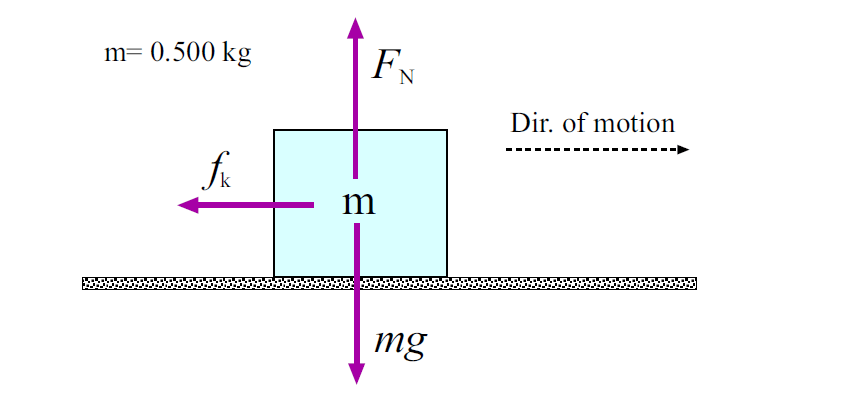
The forces acting on the block are gravity (mg, downward) the normal force from the surface (FN, upward), and the force of kinetic friction (fk, backward i.e. opposite the direction of motion).
Now, the motion only takes place along a horizontal line, so the vertical acceleration is zero. So the net vertical force on the mass is zero, giving: FN − mg = 0
=> FN = mg = (0.500 kg)(9.80 m/s2 ) = 4.90 N
Now that we have the normal force of the surface, hence the magnitude of the (kinetic) friction force:
fk = μkFN = (0.300)(4.90N) = 1.47N
(b)
The net force on the block is the friction force so that the magnitude of the block’s acceleration is
a = Fnet / m = fk /m = 1.47/0.5 m/s2 = 2.94 m/s2
[We should note that the direction of the acceleration opposes the direction of motion, so if the velocity is along the +x direction, the acceleration of the block is ax = −2.94 m/s2 ]
(c)
Now to find out the distance the block slides on the rough part before it comes to a halt we can opt for any one of the following alternatives:
alternative – 1:
using the equation v2 = u2 – 2 a x, where final velocity v=0, initial velocity = u = 2.8 m/s, and x is the distance travelled before coming to a halt.
x = u2/(2a) = 2.82/(2 x 2.94) = 1.33 m
alternative – 2:
As the block slide on the rough part, before it comes to a halt, that means its KE is equal to the work done by the friction. (friction does negative work)
(1/2) m u2 = fk . x
=> (1/2) m u2 = μk mg. x
=> (1/2) u2 = μk g. x
=> x = (1/2) u2 / ( μk g ) = (1/2) ( 2.82 ) / ( 0.3 x 9.8 ) = 1.33 m
[ in the 2nd alternative solution, the value of fk can be put directly in this case, as we have calculated it in an earlier step. ]
