Shape change by Forces & stretching a spring
Let’s discuss the application of forces to change the shape of an object and the concept of elasticity related to this shape change. We will cover the stretching of spring as a case study.
If one force only is applied to an object then the object will change speed or direction. If we want to change the shape of an object, we have to apply more than one force to it.
Forces in opposite directions will tend to stretch or compress a body.
- If two forces tend to stretch a body they are described as tensile.
- If they tend to compress a body they are known as compressive.
Figure 1 shows some examples of how balanced forces can change the shape of some objects. Because the forces balance, the objects remain stationary, but their shapes change.
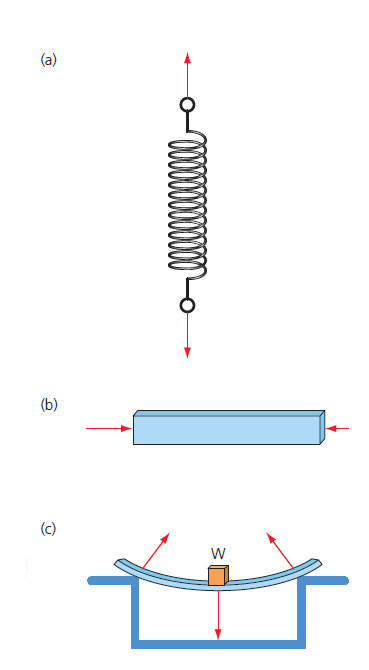
- Two balanced forces can stretch a spring. (figure 1a)
- Two balanced forces can compress a beam. (figure 1b)
- Three balanced forces cause a beam to bend. (figure 1c)
shape change and elasticity
Elastic and inelastic deformations can be shown easily by stretching a spring in the laboratory.
elastic deformation
Sometimes when an object has been stretched, it returns to its original length after the forces are removed. If this happens, the object experiences elastic deformation. When small forces are applied to stretch a spring in the laboratory and then removed, the spring returns to its original length and shape. This is an example of elastic deformation.
inelastic deformation
Sometimes an object that has been stretched does not return to its original length when the forces are removed. If the object remains permanently stretched, the object experiences inelastic deformation. When large forces are applied to stretch a spring and then these forces are removed, the spring does not return to its original length. This is an example of inelastic deformation.
You can also explore elastic and inelastic behaviour with an empty drinks can. When you squeeze the can gently, it springs back to its original shape when you remove your fingers. However, by applying larger forces you can change the can’s shape permanently.
Stretching a spring
For a spring that is elastically deformed, the force exerted on a spring F and the extension x of the spring are linked by the equation:
F = k x
=> force = spring constant × extension
where force is in newtons (N), the spring constant k is in newtons per metre (N/m) & the extension x is in metres (m).
The equation F = kx can also be applied to the compression of a stiff spring by two forces. In this case, x is the distance by which the spring has been compressed (squashed).
what is the Spring Constant
The spring constant is a measure of how stiff a spring is. If the value of k is large, the spring is stiff and difficult to stretch.
When spring has a spring constant of 180 N/m, this means that a force of 180 N must be applied to stretch the spring 1 m.
The spring constant is the force per unit extension. It is a measure of the stiffness of the spring. The larger the spring constant, the larger is the force required to stretch the spring through a given extension. The unit of the spring constant is newton per metre (Nm-1).
work done in stretching or compressing a spring | elastic potential energy formula
The work done in stretching or compressing a spring (up to the limit of proportionality) can be calculated using the equation:
Ee = (1/2) kx2
This is also the equation of elastic potential energy.
=> elastic potential energy = (1/2) × spring constant × (extension)2
sample numerical using spring constant
Example
George uses a spring to weigh a fish he has just caught. The spring stretches 8 cm.
George knows that the spring constant is 300 N/m. Calculate the weight of the fish.
Answer
k = 300 N/m
extension x = 8 cm = 0.08 m
Weight of the fish = force exerted = F
F = k x
= 300 x 0.08
= 24 N
Limit of proportionality
The graph in Figure 2 shows what happens if you put enough weights on the spring to cause inelastic deformation. There comes a point when the spring is permanently deformed, and it has gone beyond the limit of proportionality. Now when the weights are removed, the spring does not return to its original length.
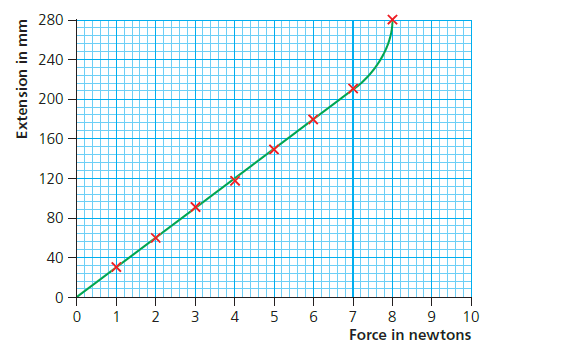
The spring constant for the spring can be calculated from the linear section of the graph by dividing the force by the extension:
k = F/x
What is Elastic potential energy?
When a spring is deformed elastically, the energy stored in the spring is called elastic potential energy. The further the spring is stretched, the greater the amount of elastic potential energy stored in the spring.
However, if an object is deformed inelastically, there is no elastic potential energy stored.
For example, when you crush a drinks can, work has been done moving atoms past each other to make a new shape. The work done causes a small temperature rise in the can.
some key terms
Limit of proportionality: The point beyond which a spring will be permanently deformed. Elastic deformation stops and inelastic deformation starts here. In Figure 2, the extension of the spring is directly proportional to the force applied, until the limit of proportionality is reached.
Elastic deformation: when an object returns to its original length after it has been stretched.
Inelastic deformation: When an object does not return to its original length after it has been stretched.
Extension: The difference between the stretched and unstretched lengths of a spring.
