Numerical Problems on Rolling motion, Torque, and Angular Momentum

Last updated on April 14th, 2021 at 01:10 pm

Here we have listed down selected numerical problems based on Rolling motion, Torque, and Angular Momentum. These are collected from standard reference books and the internet. This physics numerical worksheet contains some hard problems as well.

Numerical Problems on Rolling motion, Torque, and Angular Momentum (worksheet with medium & Hard problems)

1 ) A wheel of radius 0.25 m, moving initially at 43 m/s, rolls to a stop in 225 m. Calculate (a) its linear acceleration and (b) its angular acceleration. c) The wheel’s rotational inertia is 0.155 kg.m^2; calculate the torque exerted by rolling friction on the wheel.

2 ) A sanding disk with rotational inertia 1.2 x 10^(-3) kg.m^2 is attached to an electric drill whose motor delivers a torque of 16 N.m. Find (a) The angular momentum and (b) the angular speed of the disk 33ms after the motor is turned on.

3 ) A uniform rod rotates in a horizontal plane about a vertical axis through one end. The rod is 6.0 m long, weighs 10 N, and rotates at 240 rev/min clockwise when seen from above. Calculate (a) the rotational inertia of the rod about the axis of rotation and (b) the angular momentum of the rod.

4 ) The rotor of an electric motor has a rotational inertia Im = 2 x 10^(-3) kg.m2 about its central axis. The motor is used to change the orientation of the space probe on which it is mounted. The motor is mounted parallel to the axis of the probe, which has a rotational inertia Ip = 12 kg.m2 about its axis. Calculate the number of revolutions of the rotor required to turn the probe through 30 degrees about its axis.

5 ) Suppose that the sun runs out of nuclear fuel and suddenly collapses to form a so-called white dwarf star, with a diameter equal to that of the earth. Assuming no mass loss, what would then be the new rotation period of the sun, which currently is about 25 days? Assume that the sun and the white dwarf are uniform spheres.

6 ) A girl (mass M) standing on the edge of a frictionless merry-go-round (radius R, rotational inertia I) that is not moving. She throws a rock (mass m) in a horizontal direction that is tangent to the outer edge of the merry-go-round. The speed of the rock, relative to the ground, is v. Calculate (a) the angular speed of the merry-go-round and (b) the linear speed of the girl after the rock is thrown.

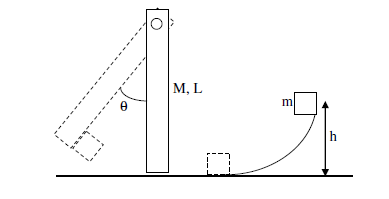
7 ) Particle m slides down the frictionless surface and collides with the uniform vertical rod, sticking to it. The rod pivots about O and rotates through the angle theta before coming to rest. Find theta in terms of the other parameters given in the figure.

8 ) A uniform sphere rolls down an incline. (a) What must be the incline angle if the linear acceleration of the center of the sphere is to be 0.10 g? (b) For this angle, what would be the acceleration of a frictionless block sliding down the incline?

9 ) A 1000 kg car has four 10 kg wheels. What fraction of the total kinetic energy of the car is due to the rotation of the wheels about their axles? Assume that the wheels have the same rotational inertia as disks of the same mass and size.

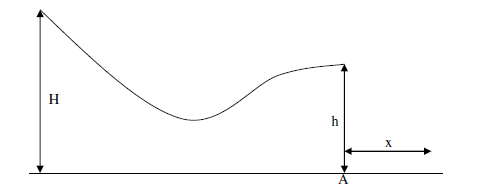
10 ) A homogeneous sphere starts from rest at the upper end of the track shown below and rolls without slipping until it rolls off the right-hand end. If H = 60 m and h = 20 m and the track is horizontal at the right-hand end, determine the distance to the right of point A at which the ball strikes the horizontal baseline.

Note: As these are for students who really look for a collection of good and hard numerical problems in physics, we are grateful and thankful to the creators of the books and sites we went through to collect these nice problems in physics, from chapters like rolling motion, rotational motion & torque and angular momentum.