How to resolve vectors easily?
Last updated on April 14th, 2021 at 02:54 pm
If we take a single vector we can find a pair of vectors at right angles to each other that would combine to give the single original vector. This reverse process is called resolution or resolving vectors. The pair of vectors are called the resolved vectors.
The resolved pair of vectors will both start at the same point as the original single vector. And as said earlier, the angle between the resolved vectors is 90 degrees and if these two resolved vectors are added following the vector addition rules then the resultant vector will be the original vector we started off with.
Steps to resolve a vector with calculations
In order to resolve a vector into a pair at right angles, we must know its size (denoting the magnitude of the vector quantity) and direction.
The direction is most commonly given as an angle to either the vertical or the horizontal. This is useful as we most commonly want to split the vector up into a horizontal and vertical pair.
Let’s take an example of a Velocity Vector which has a magnitude of 4.2 m/s and its direction makes an angle of 40 degrees with the vertical, as shown in the figure below.
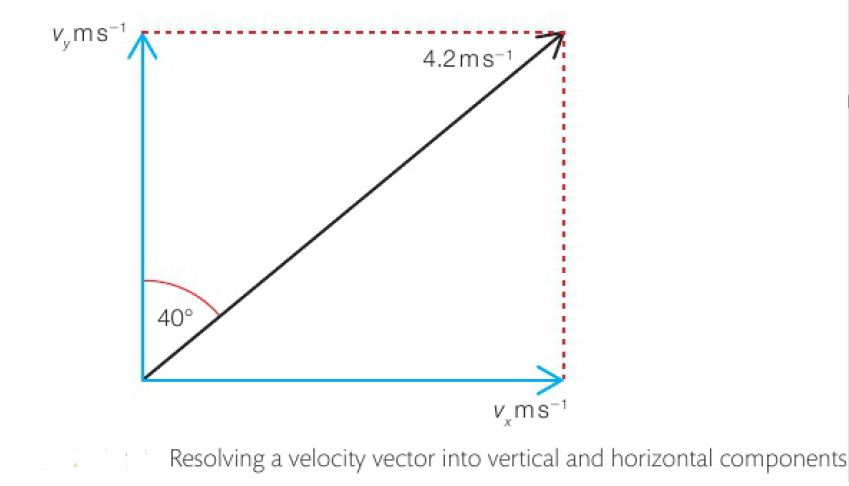
Resolving a vector Step 1 – Getting the vertical component
Redrawing components from figure 1 to show how they add up to produce the velocity vector 4.2 m/s, we get figure 2. Here we see the components making a right angled triangle.
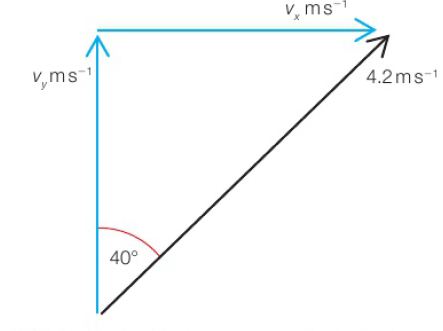
Using Trigonometry, we can say that:
cos 40 = Vy/4.2
=> Vy = 4.2 cos 40 = 4.2 x 0.766 = 3.2 m/s
Resolving a vector Step 2 – Getting the horizontal component
similarly,
Sin 40 = Vx/4.2
=> Vx = 4.2 sin 40 = 4.2 x 0.643 = 2.7 m/s
Summary:
Thus we can resolve a vector into 2 components, (1) Vertical & (2) Horizontal. Resolving a vector is an important step to solve physics numerical involving vector quantities.
Reference / Similar topics:
