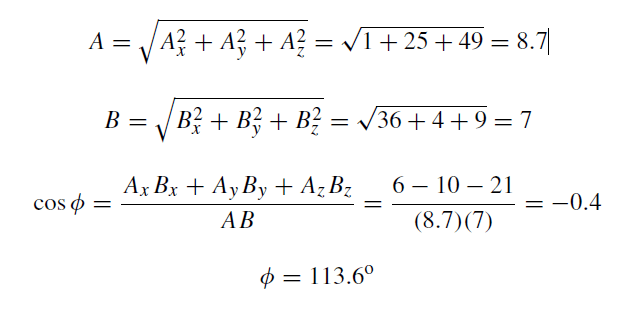How to find The Angle Between Two Vectors

In this post, we will see how to find out the angle between two vectors.

Say A and B are 2 vectors, where A =Ax i + Ay j + Azk and B = Bx i + By j + Bzk

If we take the cross product of these 2 vectors, then we can write:
A · B = (Ax i + Ay j + Azk) · (Bx i + By j + Bzk)

Using the definition of scalar product and by applying the distributive law we get nine terms:
since i · i = j · j = k · k =1, and i · j = j · k = j · k = 0, we get
A · B = Ax Bx + Ay By + Az Bz …………………. (1)

Again, as per the definition of scalar product, we can also write:
A · B = AB cos θ ………. (2) [ where θ is the angle between vector A and vector B]

from equations (1) and (2), we can write:
AB cos θ = Ax Bx + Ay By + Az Bz

cos θ =( Ax Bx + Ay By + Az Bz) / AB ……………… (3)

Using the above equation of θ we can easily find out the angle between 2 vectors.

Sample numerical problem to find the angle between 2 vectors

Example 1
Two vectors A and B are given by A = i + 5j − 7k and B = 6i − 2j + 3k. Find the angle between them.

Solution

Say the angle between A and B is φ

A · B = AB cos φ = Ax Bx + Ay By + Az Bz

cos φ =( Ax Bx + Ay By + Az Bz) / AB ………… (1)

Now let’s find out the magnitude of the 2 vectors. Then we will use these in equation 1.