Pseudo force in Physics-did you know this?
Last updated on February 12th, 2022 at 02:38 pm
What is a pseudo force? – Some forces are real, whereas others are not. Real forces have some physical origin, such as a gravitational pull, frictional force, or tension of the string. In contrast, fictitious force or pseudo force arises simply because the observer is in an accelerating or non-inertial frame of reference, such as one that rotates (like a merry-go-round) or undergoes linear acceleration (a car with acceleration or retardation).
Earth’s rotation is slow enough that Earth is nearly an inertial frame.
Pseudo force – when do we see that to act?
Let’s consider one common situation we go through almost every day.
When we ride a car and the car moves at a constant speed along a straight line (i.e. at a constant velocity as well) then we don’t feel the seat pressing against our back considerably.
This experience abides by the first law of motion which says that if there is no net force on a system then the system should move at a constant velocity.
Or in other words, if any system is moving with constant velocity, it can be assumed that there is no net force acting on the system.
Now, in this case, no net force seems to act on us horizontally, so we are sitting steadily, no pressure on our back.
Now if the car suddenly accelerates forward then immediately we feel a thrust on us in the opposite direction of the car’s movement that makes us feel that the seat is pressing against our back.
This implies that a force is applied to us. The first law of Newton makes us believe that because of this force our motion should change.
And relative to the ground outside i.e. when the observer is non-accelerating, our motion does change i.e. we seem to move with acceleration with respect to a non-accelerating observer.
But relative to the car, i.e. when the observer is a part of the accelerating frame, we can see that our motion does not change, because we remain stationary with respect to the car.
Frame of reference – pseudo force
Clearly, Newton’s first law does not hold for observers who use the accelerating car as a frame of reference.
As a result, such a reference frame is said to be noninertial.
All accelerating reference frames are noninertial.
In contrast, observers for whom the law of inertia is valid are said to be using inertial reference frames for their observations.
Now to fit Newton’s laws of motion in a noninertial frame of reference we need to bring in a fictitious force which is known as pseudo force.
In other words, when the observer is accelerating then concepts of pseudo force needs to be applied on the body being observed, to explain different situations related to motion.
Definition of a Non-Inertial Reference Frame
A non-inertial reference frame is one in which Newton’s law of inertia is not valid.
The acceleration of a non-inertial reference frame is not zero, so it moves with a velocity that changes with time.
Pseudo force – Case study 1
We will discuss pseudo force and its applications for different scenarios. The only common thing of these scenarios is that the observer is in an accelerating frame of reference. The accelerating observer may be separate from the subject of observation (which is accelerating as well) or it may be residing on the accelerating object itself.
We’ll see both types one by one. This time the observer is a part of the accelerating frame of reference
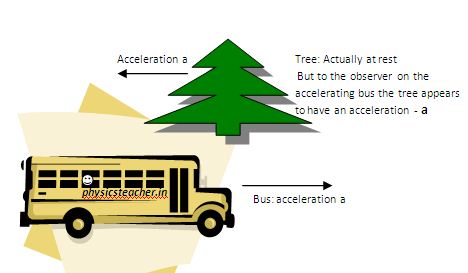
Say a passenger is sitting in a bus that is moving from left to right with an acceleration equal to 1 meter/second square.
The passenger will feel himself/herself as static with respect to the bus but at the same time to him, a mass m beside the road will seem to be moving with the same acceleration but from right to left.
This observer feels like a force appears to act on the mass m that causes the acceleration of the mass m from right to left here. Note that this is not a real force as it only appears to the accelerating observer. A static observer finds the mass m as static.
Pseudo force: calculation
So Pseudo force = mass of the body X acceleration of the observer.
So here, in this case, the Pseudo force on the mass m = m X a = ma
And the direction of this pseudo force is opposite to the direction of the acceleration of the observer.
Pseudo force – case study 2
Here we modify the above example a little bit.
We keep a box of mass m on the roof of the bus.
Also, there is a passenger sitting tightly on the roof of the bus.
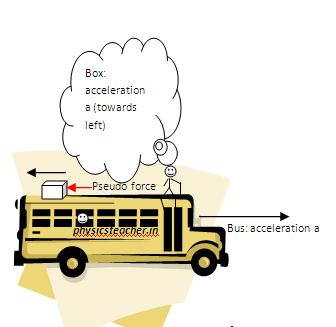
Similar to the previous example a passenger is there inside the bus as well and the bus is moving ahead with an acceleration a.
We have seen that the passenger inside the bus will feel himself stationary with respect to the bus. The passenger on the roof will also feel himself stationary with respect to the bus.
But the twist here is, the passenger on the roof will observe the box on the roof to be accelerating in the opposite direction with acceleration a.
To this passenger on the roof, it will appear like some force is pushing the box towards the left.
Yes, we call this fictitious force as the pseudo force. And in this case, we calculate the pseudo force in the same way as we did last time.
So Pseudo force = mass of the body X acceleration of the observer.
Here acceleration of the observer (i.e. the passenger on the roof of the bus) = acceleration of the bus = a.
So here, in this case, the Pseudo force on the mass m = m X a = ma
And the direction of this pseudo force is opposite to the direction of the acceleration of the observer.
Pseudo force is not a real force as it is only observed by an accelerating observer. It doesn’t obey Newton’s Laws of motion. How can we say this? Read on.
Pseudo force and Newton’s Laws of motion
Newton’s 1st law: As per this law when there is no net force on a system, then that system can not have any acceleration. Pseudo force violates this as without any external force an object started to accelerate. (appears to be so as described above). It violates the first law of motion.
Newton’s 2nd law: This law gives the equation of force which is equal to mass X acceleration. In the case of Pseudo force, we don’t have any applied net force. But we find the acceleration of a body with some mass. I.e. when Force is zero, mass and acceleration are nonzero. It violates the 2nd law.
Newton’s 3rd Law: There is no existence of any reaction force of this pseudo force. So it violates the 3rd law as well.


