Elevator problems in physics with pseudo force

Last updated on April 16th, 2021 at 10:17 am

Elevator problems in physics with pseudo force – When an elevator is moving with an acceleration, it becomes a non-inertial frame of reference. We find it difficult to apply Newton’s laws of motion for a non-inertial frame of reference when the observer is a part of that reference. Here we will discuss the contribution of the concepts of pseudo force and discuss elevator physics with pseudo force. Once we start applying this concept, we can solve elevator physics problems with ease! Now you may read it with a cup of tea!

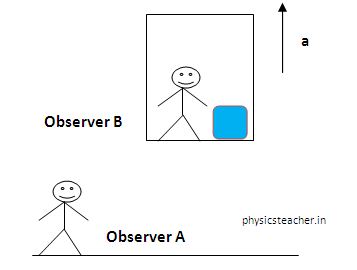
Observer B is in an elevator. The elevator is moving upwards with an acceleration a. A box of mass M is resting on the elevator floor.

Observer A is stationary and standing on a static surface (say ground) and watching the box on the elevator floor.(the elevator has glass walls 🙂 )

Both observer B and the box are moving upwards with an acceleration a.

So the observer A (who is on the inertial frame of reference) will draw the Free Body Diagram (FBD) of the box on the elevator floor in this way:

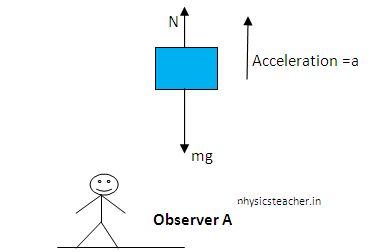
In the FBD, N is the Normal reaction exerted by the elevator floor on the box. The gravitational pull on the box is mg. (m is the mass of the box and g is the acceleration due to gravity)

Observer A will observe the box in the elevator to move upwards with an acceleration a.
So he will write the net force equation following Newton’s Second Law of motion in the following way:

Net force = N – mg
we know, Net force = mass X acceleration = m a
hence, ma = N – mg
or, N = m (g + a) …………………………………  (1)

Now we take observer B, who is traveling with the box in the same elevator.

As both observer B and the box are within the same elevator frame of reference, observer B will find the box to be static. So for observer B, the acceleration of the box equals zero.
Now observer B will draw the FBD of the box in the following way:

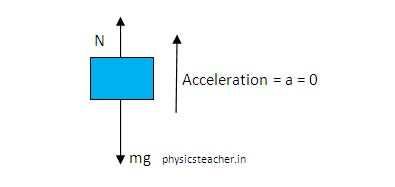
Observer B also will write motion equations following Newton’s 2^nd law.

N – mg = Net force
Net force = mass X acceleration = m x 0= 0  ( as the box appears to be static to observer B)
hence, 0 = N – mg
or, N = m g …………………………………  (2)

2 observers are giving different observations and interpretations of Newton’s law. We know why. Observer A watches the motion of the box from an inertial frame of reference. And we have read in one of our earlier posts that Newton’s laws are well applicable in inertial frame of reference.

On the contrary observer B watches the box being a part of an accelerating or non-inertial frame of reference. And we know this type of frame of reference doesn’t directly support the Newton’s laws of motion, when the observer is also a part of the system.

Then what to do for the non-inertial frame of reference while solving numerical? Yes, you are right.
We have to incorporate the concept of Pseudo force.
Let’s see how we can do the same here in this case.

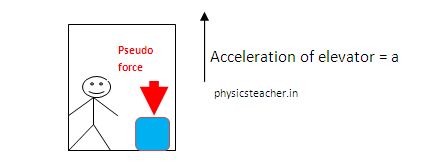
Now following the concept of pseudo force we can get the magnitude and direction of the pseudo force on the box. Note that here the observer B is having an acceleration a upwards. (as the elevator he is in is moving with that acceleration)

Pseudo force on the box = mass of the box X acceleration of the observer B = m a
Direction of this force = opposite to that of the reference frame = downwards

want a quick revision? read this:

pseudo force

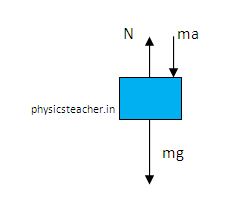
Now with the inclusion of pseudo force if we draw the FBD of the box for observer B then see what we find.

So now for observer B we write equation:
Net force = N – mg – ma

As observer B finds the box static so a = 0

So Net force on box = 0

As a result, N – mg – ma = 0
hence, N = m ( g + a) ………………………….. (3)

So we have just seen how just by including the concept of pseudo force we can successfully apply Newton’s 2nd law of motion even in an accelerating non-inertial frame of reference.

Good Read for U: 

Inclined Plane (wedge) and Pseudo force

Concepts of pseudo force