Viscosity – definition, derivation, coefficient of viscosity

Last updated on December 15th, 2021 at 09:18 pm

Here we will define & discuss the concepts of viscosity and derive the formula of the coefficient of viscosity.

When we pour a glass of water, it flows freely and quickly. But when we pour honey that flows slowly and sticks to the container.
The cause behind this difference is fluid friction, both within the fluid itself and between the fluid and its surroundings (say container wall). We call this property of fluids Viscosity.

Obviously from the behavior of water and honey, we can say that water has low viscosity, whereas honey has a higher one. Now let’s find more details on this fluid friction.

---

---

Viscosity – definition

The viscosity of a fluid relates to its stickiness and thus to its resistance to flow. Syrup and engine oil are very viscous, while runny liquids such as water and petrol and all gases have low viscosities. Viscosity can be described in terms of the resistance between adjacent layers in laminar flow.

Friction and Viscosity

When a block slides across a rough floor, a frictional force between the block and floor opposes the motion.

Similarly, a fluid flowing past a stationary surface experiences a force opposing the flow. This opposing force also exists when two adjacent layers of fluid have to move relative to each other. This tendency to resist a fluid flow is referred to as the viscosity of a fluid.

Fluids like air have low viscosities, thicker fluids like water are more viscous, and fluids like honey and motor oil are characterized by high viscosity.

Ideal fluid and Viscosity

Fluid flow can be compressible or incompressible. Most of the liquids are nearly incompressible as the density of a liquid remains almost constant as the pressure changes.

So we can approximately say, then, liquids flow in an incompressible manner. In contrast, gases are highly compressible with some exceptions though.

Fluid flow can be viscous or nonviscous.

The flow of a viscous fluid is an energy-dissipating process.

The viscosity resists neighboring layers of fluid from sliding freely past one another.

A fluid with zero viscosity flows in an unhindered manner with no dissipation of energy.

Although no real fluid has zero viscosity at normal temperatures, some fluids have negligibly small viscosities.

Then what is an ideal fluid?

An incompressible, nonviscous fluid is called an ideal fluid. An ideal fluid is also assumed to have steady (laminar flow) and irrotational flow.

Ideal fluid with zero viscosity vs real fluid

Let’s take a type of flow—say the flow of a fluid through a tube. Examples of this type of flow can be (1) water flowing through a metal pipe in a house and (2) blood flowing through an artery or a vein.

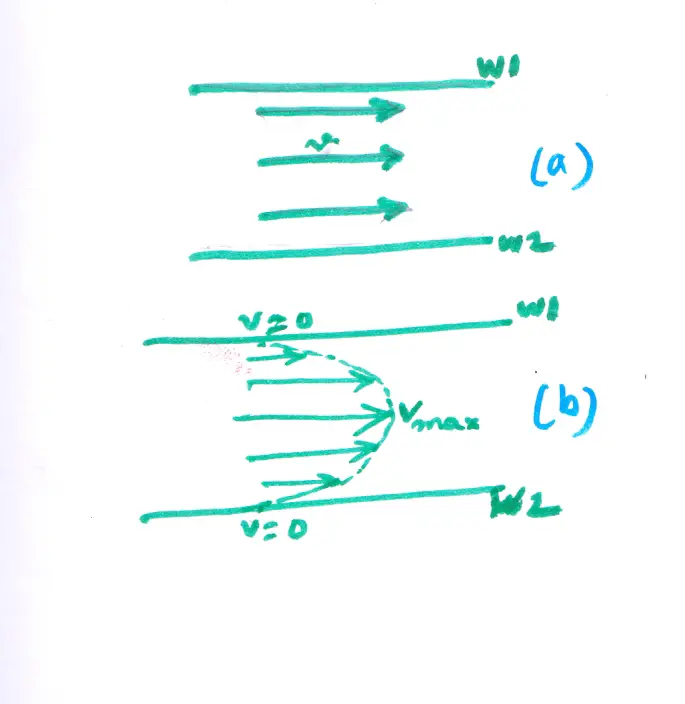
If the fluid were ideal, with zero viscosity, it would flow through the tube with a speed that is the same throughout the fluid, as indicated in Figure 1(a)

Real fluids with finite viscosity are found to have flow patterns like the one shown in Figure 1(b). In this case, the fluid is at rest next to the walls of the tube and flows with its greatest speed in the center of the tube. We will discuss this in detail below.

Coefficient of Viscosity – derivation of formula

In an ideal fluid, there is no viscosity to resist the fluid layers as they slide past one another.

Within a pipe of uniform cross-section, every layer of an ideal fluid moves with the same velocity, even the layer next to the wall, as Figure 1(a) shows.

When the viscosity is present, the fluid layers have different velocities, as figure 1(b) illustrates. The fluid at the center of the pipe has the greatest velocity. In contrast, the fluid layer next to the wall surface does not move at all, because it is held tightly by intermolecular forces.

So strong are these forces that if a solid surface moves, the adjacent fluid layer moves along with it and remains at rest relative to the moving surface.

Mathematical expression or formula of viscosity

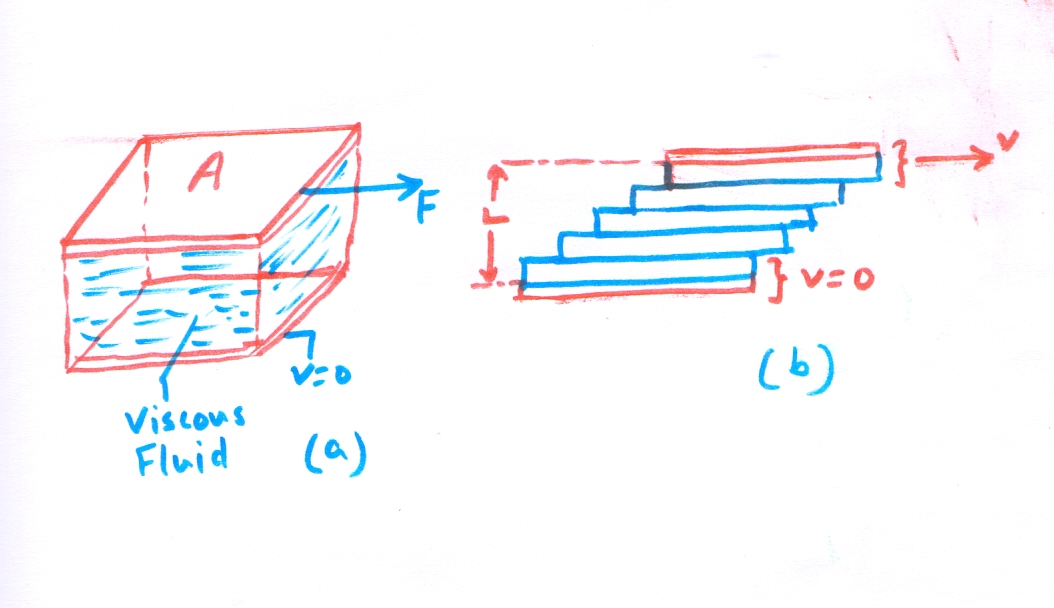
To find out a mathematical expression or formula, Figure 2(a)  shows a viscous fluid between two parallel plates.

The top plate is free to move, while the bottom one is stationary.
If we want to move the top plate with a velocity relative to the bottom plate, a force F is required.

** For a highly viscous fluid, like thick honey, a large force is to be applied; for a less viscous fluid, like water, a smaller one will do.

As part 2 (b )of the drawing suggests, we may imagine the fluid to be composed of many thin horizontal layers.

When the top plate moves, the topmost fluid layer, adjacent to the top plate, moves along the top plate. The reason is the strong intermolecular forces.

At the same time, the intermediate fluid layers slide over each other.

The velocity of each layer is different, changing uniformly from zero at the top plate, then gradually rising to a max value at the centremost layer and then again reducing gradually to zero at the bottom plate.

The resulting flow is called laminar flow since a thin layer is often referred to as a lamina.

As each layer moves, it is subjected to viscous forces from its neighbors.

The purpose of the force F is to compensate for the effect of these forces so that any layer can move with a constant velocity.

Now, let’s focus on the factors on which this force F depends.

The amount of force required in Figure (2) depends on several factors.

*  F is proportional to the area A of the plate. This relationship holds good since A is directly proportional to the amount of fluid being moved.

* For a given area, greater speeds require larger forces. So the force F is proportional to the speed (v).

* The force is also inversely proportional to the perpendicular distance L between the top and bottom plates (F varies with 1/L). The larger the distance L, the smaller is the force required to achieve a given speed with a given contact area. L is like a lever arm, and the greater the lever arm, the less force that is needed.

And F is directly proportional to the viscous nature of the fluid or coefficient of viscosity, η (eta). The greater the viscosity, the greater the force required to move the fluid.

These 4 dependencies are combined into the equation

F = ηvA /L ………………….(1), which gives us a working definition of fluid viscosity η.

Solving for η, which is called the coefficient of viscosity or simply the viscosity, gives

η= (FL)/(vA) ………………………(2)

which defines viscosity in terms of how it is measured. The SI unit of viscosity is N ⋅ m/[(m/s)m^2 ] = (N/m^2)s or Pa ⋅ s.

From equation 1, we can say that the effort required to move fluid (like pouring) depends on its viscous nature, labeled by η or coefficient of viscosity. Honey has a higher value of η than that of water, hence pouring honey needs a little more effort compared to pouring water.