Orbital Velocity Formula with solved numerical problem
Last updated on February 12th, 2022 at 03:08 pm
Here in this post, we will list down different forms of the Orbital velocity formula or equation. We will present here 3 sets of formulas including the near-orbit one. After this, we will also see how to use these formulas to solve numerical problems.
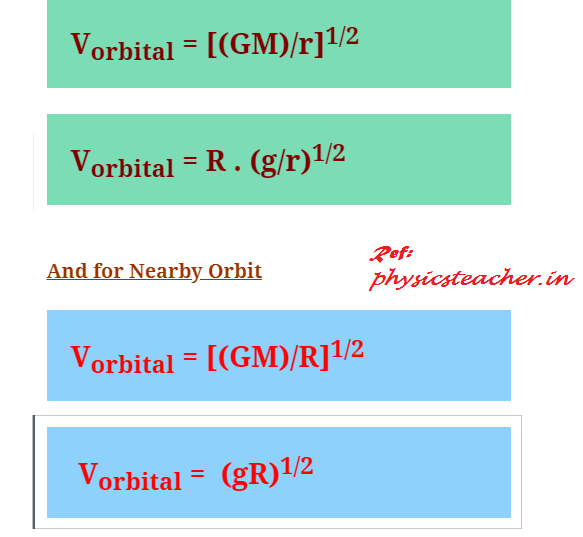
Orbital Velocity Formula – 3 sets of formulas are listed below:
Orbital Velocity Formula Set 1:
V = [(GM)/r]1/2 ……………. (1)
( here G = gravitational Constant,
M is the mass of the central body i.e. for the formula of the orbital velocity of the earth’s satellite, M denotes the mass of the earth,
Here R = radius of the earth, h = height above the earth’s surface, And r = R +h )
Orbital Velocity Formula Set 2:
V = R . (g/r)1/2 ……. (2)
(Here R = radius of the earth, h = height above the earth’s surface, And r = R +h )
Orbital Velocity Near Orbit equation Set 3: [ for near-orbit satellite]
(2 expressions for Near Orbit)
V = [(GM)/R]1/2 ———–(3)
Vorbital =(gR)1/2……….(4) here, R =radius of the earth
Formula sets (Graphical Representation)
Derivation of the above-listed formula
Sample Numerical problem based on Orbital velocity equation – with solution
Q) Assume that a satellite orbits Earth 225 km above its surface. Given that the mass of Earth is 5.97 x 1024 kg and the radius of Earth is 6.38×106 m, what is the satellite’s orbital speed?
Solution:
h =2.25×105 m (height of the satellite’s orbit)
rE =6.38×106 m (Earth’s radius)
mE =5.97×1024 kg (Earth’s mass)
G = 6.67×10-11 Nm^2/kg^2
Orbital velocity = V =?
We get the orbital radius r by adding the height of the satellite’s orbit to Earth’s radius.
r =h +rE =2.25×105 m + 6.38×106 m = 6.61×106 m
So, Orbital speed.
V = √[(G mE)/r] = [G mE)/r ]1/2 = 7.76 x 103 m/s
Related Posts for you
Derivation of the above-listed formula
Definition
