Terminal Velocity, Free Fall, & Drag force
Last updated on May 16th, 2022 at 08:30 pm
Here we will discuss in detail the terminal velocity and Terminal Velocity Equation. Before that, we will also cover a few important pointers on free fall and then discuss Air Drag or Air resistance, Drag force, and Drag Force Equation. In one of the earlier posts, we have discussed the free-fall equations. You can check that if you want at this point.
Freefall and air resistance(air drag) – FAQs and answers
What is a free fall?
From the name itself, we can see, there are 2 things. ‘Fall’ and ‘Free fall’.
We know objects, when thrown normally upwards, comes downwards after a while, so it’s a fall.
And we all know the reason behind this fall. That is Gravity or Gravitational force between the earth and the object in discussion.
Now ‘Free fall’ means, the fall of the object from a height is free from all resistance.
In Newtonian motion, Freefall is the motion of a body when the sole force acting on the body is Gravity.
So when we discuss a free fall or solve a numerical related to it, we consider air resistance as zero.
Free fall equations
The free-fall equations resemble the equations of linear motion, here in place of acceleration (a) we use the acceleration due to gravity (g). You may go through this post to read in details: Freefall Equations
Free Fall and Weightlessness
During Freefall as there is no surface to provide the Normal Reaction Force on the freely falling body, the falling body has the feeling of weightlessness. But remember that, this is a feeling only and gravity continues to work on the falling body. Read on weightlessness.

Practicality of a Free Fall
Now practically we can consider air resistance as zero only when it’s found Negligible! Couple of situations can be considered for this.
1) height from where the fall is happening is very small.
2) speed of the falling object is small.
3) area of the surface facing air resistance is small.
4) density of the falling object is considerably high.
5) shape of the object is such (aerodynamic) that it cuts through the air without much resistance.
When an object is dropped from a height and that in vacuum then this free fall is observed actually!
Falling in a vacuum
Air drag or air resistance is caused by collisions of air particles with a falling object. In a vacuum, as there is no air particle, the air drag is absent there. As a result, the net force acting on the falling body is gravity.
Here, we can write F (net) = W
=> ma = mg
=> a = g
That means the acceleration of the falling object in a vacuum is independent of its mass.
That’s why when a hammer and a feather are released in a vacuum from a height, then both of them fall at the same rate and hit the ground at the same time.
In 1971, Apollo 15 astronaut David Scott dropped a hammer and a feather from the same height while standing on the surface of the Moon (yes, scientists really did pack a hammer and a feather on the spacecraft just so they could test this). The hammer and the feather fell at the same rate and hit the ground at the same time.
As discussed in the previous section, drag is caused by collisions of air particles with a falling object.
The Moon’s gravity is too low to hold a thick atmosphere around it like the Earth can, so the hammer and the feather both fell without encountering enough particles to cause any measurable drag. The masses of the two objects had no influence at all on the rate at which the objects fell.
They both fell at about 1.6 m s−2 (the acceleration due to gravity on the Moon) and hit the dust (literally) at the same time.
What this little experiment on the Moon proved was that Galileo’s theory was correct. In a vacuum, all objects will fall at the same rate, regardless of mass and size.
Drag Force
Now when an object is falling through the atmosphere from a high altitude, then we can no more ignore the air resistance force. This means 2 forces are now acting simultaneously on the object.
As per Newtonian concepts, it’s no more a Freefall.
An opposing resistive air force also called Drag Force, is now active on the falling object, apart from the downward gravity force.
Drag is caused by the collision of a falling object with the particles in the air; this has the effect of slowing the object’s descent. The greater the number of particles that the object collides with, the greater the size of the drag it experiences.
Two forces acting on a falling body are gravity and air drag
Gravity or weight:
Gravity is equal to the weight (W) of the falling body. If the mass of the body is m and g is the acceleration due to gravity (9.8 m/s^2), then Gravity is equal to the weight W of the object, where
Gravity=W= mg…… (1)
Air drag:
The Air Drag is like frictional force opposing the motion but its formula is different from Friction. This air drag depends on few factors, which are all present in its equation.
Drag Force equation
Drag Force = D = 0.5 * K * r * V2 * A ………. (2)
[This is the Drag force formula ]
here K = Drag Coefficient of the falling object (it depends on the inclination of the shape and some other criteria like air flow)
r = air density
V= velocity of the falling object
A = cross sectional area of the object falling
Here we can see that this Drag increases with the increase in velocity (as square of the velocity).
The value of Drag force depends on these quantities:
The drag force exerted on an object is directly proportional to the following:
- The drag force exerted on an object is directly proportional to the object’s cross-section perpendicular to its direction of motion. An object with a large cross-section will collide with more air particles than one with a small cross-section, so it would experience a greater drag.
- The drag force exerted on an object is directly proportional to the density of the air through which the object moves. Close to the Earth’s surface, the air has a density of about 1.2 kg m−3, which is much denser than at, say, an altitude of 10 km, where the air density is around 0.4 kg m−3. This means that an object falling at the 10 km mark will collide with fewer particles and so will experience less drag than an object falling nearer the ground.
- The drag force exerted on an object is directly proportional to the square of the object’s speed. An object traveling at a speed of 10 m s−1 will encounter four times the magnitude of the drag than if it were to travel at 5 m s−1.
Drag is also affected by the object’s shape, the smoothness of its surface, and the amount of turbulence that these factors cause in the air as the object falls.
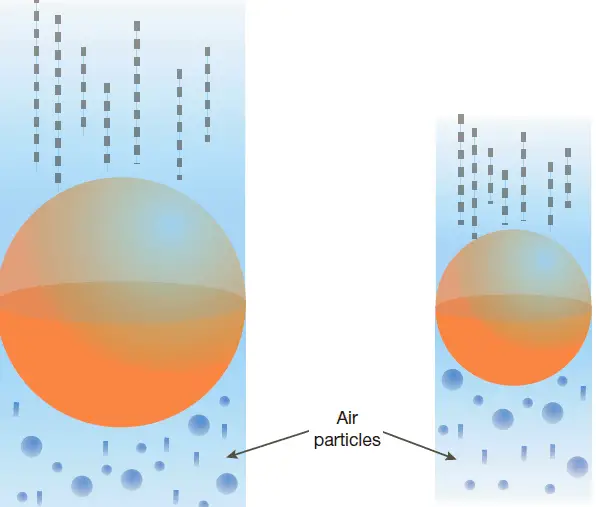
with more air particles than one with a smaller cross-section.
Gravity Vs Drag
Now for a falling body, Gravity and this Drag force work in the opposite direction.
Hence the net force on the falling object is F = W – D ….. (3)
As there is a net force on the falling body, it will certainly have an acceleration, which is a = (W – D) / m
Please note that this acceleration is different from g (acceleration due to gravity).
As the body is under acceleration, so certainly its velocity will rise with time. As the velocity increases, the Drag Force goes on increasing. (See equation 2)
W remains constant throughout the fall.
At some point, if time of the fall permits, D becomes equal to the weight or gravity W.
Here the net force on the falling object becomes zero and acceleration becomes 0.
That means now onwards the falling object falls with a constant velocity.
W – D = 0;
so, W = D ……………………………. (4)
Formation skydivers spread their limbs out to increase their surface area perpendicular to their direction of fall. This increases their drag, which decreases their descent speed, extending the time that they are in the air.

Terminal Velocity
Net force on the falling object if becomes zero means, no acceleration of the falling object at that moment.
As per Newton’s First Law, in this scenario the object falls with a constant downward velocity.
This constant velocity directing vertically downwards is called Terminal Velocity.
So what we have seen here is that
A falling object, under the influence of gravity and Drag force, falls with an acceleration, which is not equal to g. As the falling object gains velocity while falling, it attains a velocity that results in zero net force on the falling object. This specific velocity of the falling object is called Terminal Velocity.
As said above, once a falling object attains the terminal velocity, Net Force on it becomes zero. As a result, its downward velocity becomes constant i.e. at terminal velocity acceleration of the falling object is zero.
Terminal Velocity Equation
From the above equations, we get the equation for Terminal Velocity.
In this case, W = D
so, W = 0.5 * K * r * V^2 * A
Here we get Terminal Velocity Equation or formula:
Terminal Velocity = V =[(2 * W) / (K*r*A)] 1/2 …………………… (5)
Terminal Velocity =
V =[(2 * W) / (K*r*A)] 1/2
[formula for Terminal Velocity]
here K = Drag Coefficient of the falling object (it depends on the inclination of the shape and some other criteria like airflow)
r = air density
W = weight of the falling object
A = cross sectional area of the object falling
Terminal Velocity – Factors
Terminal Velocity varies directly with the weight of the object. (see equation 5)
Let’s take 2 objects with the same shape and size but with different weights. The heavier object will attain a higher terminal velocity. That means the heavier object falls faster than its lighter contestant, once terminal velocity is attained by both the objects. (**Please note that, in a vacuum where there is no air resistance or drag, both these objects would fall with the same velocity)
An object with a large cross-sectional area will fall slower than an object with a smaller area. (see equation 5, Area A is in the denominator)
Again an object with a higher drag coefficient falls slower than an object with a lower drag coefficient. (see equation 5, K is in the denominator)
Continue Reading the Related Posts

