The differences between Uniform circular motion and projectile motion with diagrams
Last updated on June 5th, 2021 at 08:04 pm
The acceleration in a uniform circular motion (Fig. 1) has some similarities to the acceleration in projectile motion (Fig. 2) without air resistance, but there are also some important differences between Uniform circular motion and projectile motion.
Differences between Uniform circular motion and projectile motion
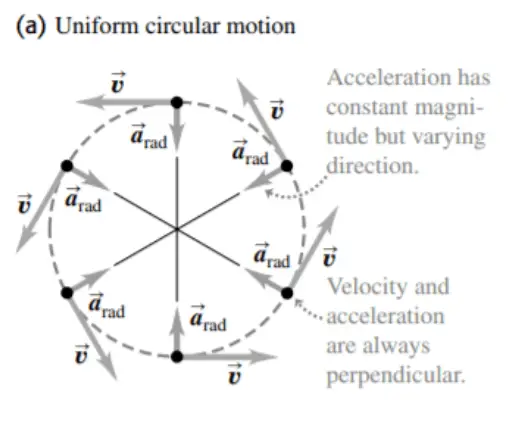
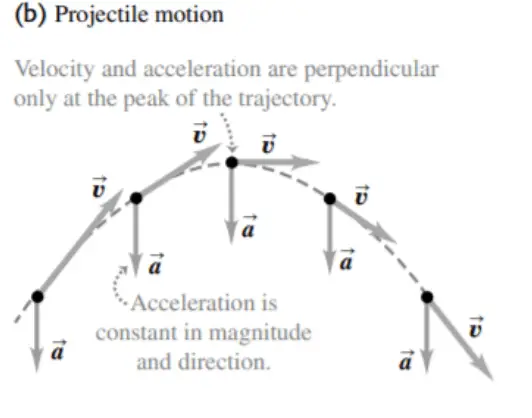
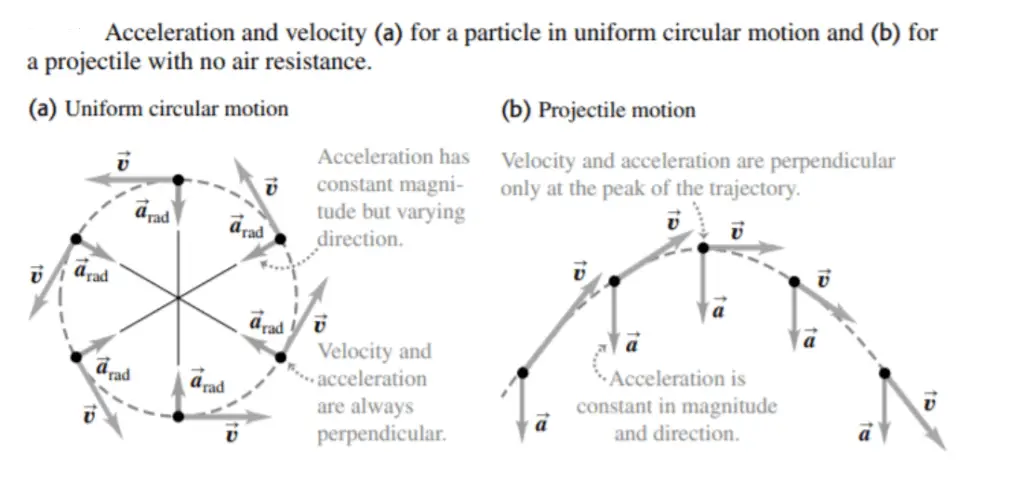
1) In both kinds of motion, the magnitude of the acceleration is the same at all times.
However, in a uniform circular motion, the direction of acceleration changes continuously so that it always points toward the center of the circle. (For example, At the top of the vertical circle the acceleration points down; at the bottom of the vertical circle the acceleration points up.)
In projectile motion, by contrast, the direction of acceleration remains the same at all times.
2) In Uniform Circular Motion the direction of velocity is always perpendicular to the direction of acceleration. But, for projectile motion velocity and acceleration are perpendicular only at the peak of the trajectory.
3) We can also express the magnitude of the acceleration in a uniform circular motion in terms of the period T of the motion, the time for one revolution (one complete trip around the circle). In a time T the particle travels a distance equal to the circumference 2πR of the circle of radius R, so its speed is v= 2 π R/T
When we substitute this into the equation of centripetal acceleration, we obtain the alternative expression of it as:
arad = mv2/R = m (2 π R/T)2 /R = m 4 π2 R /T2.
No similar kind of time period concept or equation is there for projectile motion.
Suggested Reading:
Projectile motion – detailed Notes & equation derivation
Uniform circular motion & centripetal force

