Uniform Circular motion

Last updated on August 25th, 2023 at 01:03 pm

In this post, we will cover a bunch of questions and equations from the Uniform Circular Motion chapter.

When a particle moves in a circle with constant speed, the motion is called uniform circular motion.

Examples of uniform circular motion: A car rounding a curve with a constant radius at a constant speed, a satellite moving in a circular orbit, and an ice skater skating in a circle with constant speed are all examples of uniform circular motion.

---

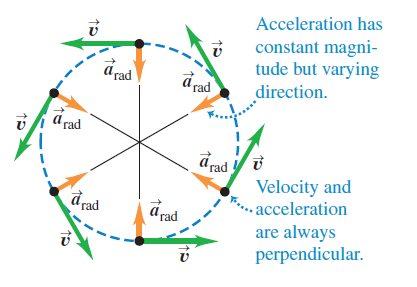
Direction of the Acceleration in a uniform circular motion

There is no component of acceleration parallel (tangent) to the path; otherwise, the speed would change.

The acceleration vector in uniform circular motion is perpendicular (normal) to the path and hence directed inward (never outward!) toward the center of the circular path. This causes the direction of the velocity to change without changing the speed.

This acceleration is instantaneous acceleration.

Hence, In other words: The direction of the instantaneous acceleration at each point in a uniform circular motion is always along a radius of the circle, toward its center.

Magnitude of the instantaneous acceleration in a uniform circular motion

In a uniform circular motion, the magnitude a of the instantaneous acceleration is equal to the square of the speed v divided by the radius R of the circle. Its direction is perpendicular to v and inward along the radius.

a = v² / R

Why do we call the acceleration centripetal for circular motion?

Because in the case of uniform circular motion, the acceleration is always directed toward the center of the circle, it is sometimes called centripetal acceleration. The word ‘centripetal’ is derived from two Greek words meaning ‘seeking the center’.

ω = θ/t = 2π / T

Angular velocity formula in terms of time period T

Thus we get the Angular velocity formula in terms of time period T as:
ω = 2π / T

Linear speed formula in terms of time period T (for circular motion)

The time for one revolution (one complete trip around the circle) = T.
In a time T, the particle travels a distance equal to the circumference 2πR of the circle.
Hence, the linear speed v of an object in a uniform circular motion can be expressed by this formula:

v = 2πR / T

Magnitude of the acceleration in a uniform circular motion in terms of the time period

The magnitude of the acceleration in a uniform circular motion in terms of the time period can be derived in the following way:

a = v² / R = [ 2πR / T ]² / R = 4 π²R² / (T² R )
a = 4 π²R / T²