Derive the relation between Angular Velocity and Linear Velocity

Last updated on February 8th, 2024 at 10:25 am

In this post, we will derive the Relationship between angular velocity and linear velocity.

During the circular motion, an object experiences angular displacement as well as linear displacement, therefore it will have angular velocity as well as linear velocity at any position on the circle.

The direction of the linear velocity of the rotating object at any point is along the tangent to the circle drawn at the point where the object is positioned at that moment on the circumference of the circle.

And angular velocity is being made by changing the angular position with time.

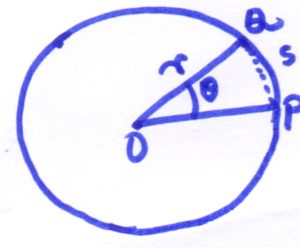
Angular velocity is identified with the sign omega (ω). And ω = θ/t  _________(1).

At the same time, we can calculate the linear velocity as the following:

linear velocity (v) = linear displacement per unit time = s/t
v = s/t ……………..(2)

We have already proved in a different post that s =θ r. You can see it here: Derivation of the relationship between angular and linear displacement.

v = s/t = (θ r)/t= (θ/t). r=ω.r   

=> v=ω.r ___________________(4)

Linear Velocity = Angular Velocity x radius