Velocity from a Displacement-Time Graph – how to derive?

Velocity is the ratio of the displacement and the time duration. Hence, velocity can be obtained from the gradient of a displacement-time graph.

Velocity = gradient of displacement-time graph

Drawing a displacement-time graph from a set of data

Let’s take a case study of a toy car that moves along a straight track. Its displacement at different times is shown in the table below. Then we will use this data to draw a displacement-time graph from which we can deduce the car’s velocity.

Displacement s (m)	1	3	5	7	7	7
Time t (s)	0	1	2	3	4	5

Now we can plot the displacement-time graph as the following one.

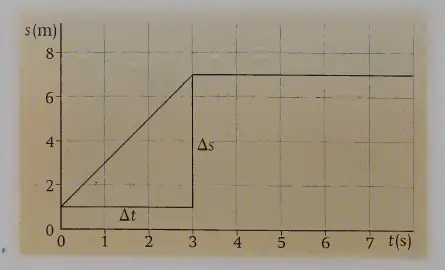
Deriving velocity from a displacement-time graph

We draw a right-angled triangle as shown. Now, to find the car’s velocity, we need to divide a displacement by a time. These are given by the two sides of the triangle labeled Δs and Δt.

Velocity v = change in displacement/change in time = Δs/Δt = (7-1)/(3-0) = 6/3 m/s = 2 m/s

Summary:

The gradient of a displacement-time graph gives velocity.
v = Δs/Δt