3 different types of vertical projectile motion

Last updated on February 8th, 2024 at 10:12 am

3 different types of vertical projectile motion are:
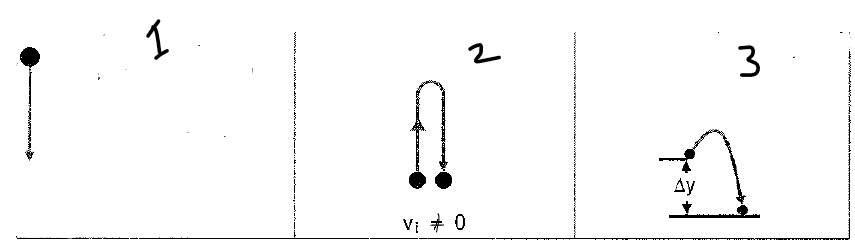
1) Vertical downward projection from a starting point above the ground –
– In this case, the object can be dropped (Initial velocity = 0)
– or it can be thrown downwards at an initial velocity >0
2) Vertical Upward Projection from a starting point at the ground level; the object turns around and returns to the starting point.
3) Vertical Upward Projection from a starting point above the ground; the object goes to the highest point and then turns, and moves downwards past the starting point towards the ground.

Signs of velocity, displacement, and g

Here, we will use these signs for understanding: V_i and V_f are the initial and final velocities respectively

Case 1: Vertical downward projection from a starting point above the ground

If the object is dropped then: V_i = 0 and V_f = positive
Downward displacement: Positive
g=9.8 m/s²

If the object is thrown downward then: V_i = positive and V_f = positive
Downward displacement: Positive
g=9.8 m/s²

Case 2: Vertical Upward Projection from a starting point at the ground level; the object turns around at the highest point and returns to the starting point

Considering the upward direction as positive, and the downward direction as negative:
V_i = positive and V_f = negative
V_f = – V_i
Net displacement: zero
g= – 9.8 m/s²

Considering the upward direction as negative, and the downward direction as positive:
V_i = negative and V_f = positive
V_f = – V_i
Net displacement: zero
g= + 9.8 m/s²

Case 3: Vertical Upward Projection from a starting point above the ground

Considering the upward direction as positive, and the downward direction as negative:
V_i = positive and V_f = negative

Net displacement: negative*
g= – 9.8 m/s²

Considering the upward direction as negative, and the downward direction as positive:
V_i = negative and V_f = positive
V_f = – V_i
Net displacement: positive*
g= + 9.8 m/s²

* The starting point can be taken as the reference point (zero).
If this is so, then a displacement below the starting point will have the same sign as the downward motion. A displacement above the starting position will have the same sign as the upward motion.