Electric field due to two infinite plane parallel sheets of charge

Last updated on May 11th, 2022 at 09:19 am

Consider two infinite plane parallel sheets of charge A and B, having surface charge densities equal to σ₁ and σ₂ respectively. (see the figures 1 to 4 in the following sections).

Note that, In a sheet of charge, the same charge shows up on its two sides. On the other hand, since a plane & charged conductor has a finite thickness, different charges show up on its two sides.

In the first 2 cases below, we talk about sheets of charge. And, in the last 2 cases, we discuss the plane charge conductor with finite thickness.

[ you may quickly refer to our post on the Electric field due to a plane sheet of charge: formula & derivation]

The two sheets (sheet 1 and sheet 2 as per the diagram below) divide the space into 3 regions:
(i) region 1 at the left of sheet 1
(ii) region 2 between sheet 1 and sheet 2 and
(iii) region 3 at the right of sheet 2

---

Electric field due to two infinite plane parallel sheets of positive charge

Here, we will consider the Electric field due to two infinite plane parallel sheets of positive charge (both sheets are positively charged). Refer to figure 1. Note: In a sheet of charge, the same charge shows up on its two sides.

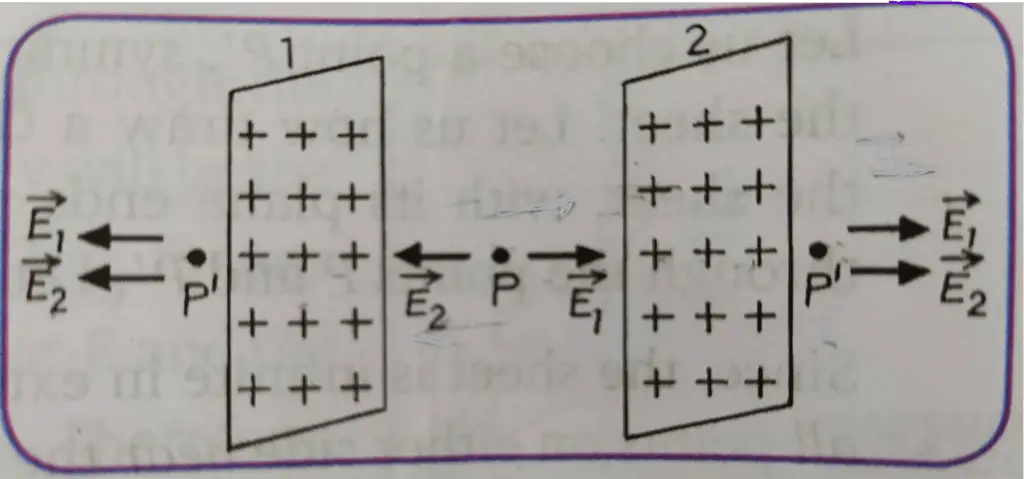
Now, consider point P’ in region 1 and point P’ in region 3 in figure 1.

[Note: (i) region 1 at the left of sheet 1 (ii) the region 2 between sheet 1 and sheet 2 and (iii) the region 3 at the right of sheet 2.]

At both these 2 points, the net electric field can be found as the sum of the electric field due to sheet 1 and the electric field due to sheet 2, because at these 2 points the directions of the electric field due to sheet 1 and the electric field due to sheet 2 are same.

[ related post for quick reference Electric field due to a plane sheet of charge: formula & derivation]

At point P’ in region 1:

|E| = (σ₁ + σ₂)/(2ε₀) ……………. (1)

The direction of the electric field is towards the left. [see figure 1]

And at point P’ in region 3:

|E| = (σ₁ + σ₂)/(2ε₀) ………….. (2)

The direction of the electric field is towards the right. [see figure 1]

Now let’s find out the electric field at P (in region 2, between 2 sheets of positive charges)

At this point, the net electric field can be found as the difference between the electric field due to sheet 1 and the electric field due to sheet 2, because at these 2 points the directions of the electric field due to sheet 1 and the electric field due to sheet 2 are opposite.

And at point P in region 2:

|E| = (σ₁ – σ₂)/(2ε₀) ……………. (3)

The direction of the electric field will depend on the values of σ₁ and σ₂.

Electric field due to two infinite plane parallel sheets of opposite charge

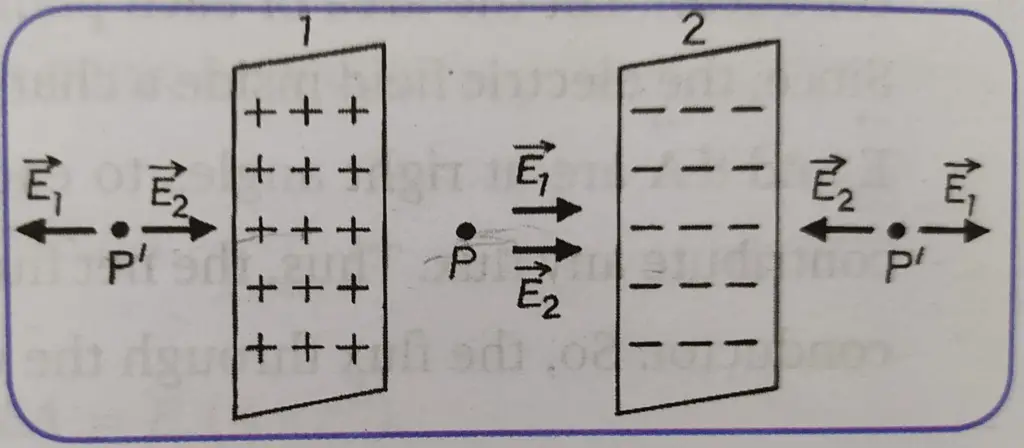
Here, we will consider the Electric field due to two infinite plane parallel sheets where one of the sheets (Sheet 1) is positively charged and the other one (sheet 2) is negatively charged. Refer to figure 2. Remember that, in a sheet of charge, the same charge shows up on its two sides.

Now, consider point P’ in region 1 and point P’ in region 3 in figure 2.

[Note: (i) region 1 at the left of sheet 1 (ii) the region 2 between sheet 1 and sheet 2 and (iii) the region 3 at the right of sheet 2.]

At both these 2 points, the net electric field can be found as the difference between the electric field due to sheet 1 and the electric field due to sheet 2, because at these 2 points the directions of the electric field due to sheet 1 and the electric field due to sheet 2 are opposite.

At point P’ in region 1:

|E| = (σ₁ – σ₂)/(2ε₀) ……………… (4)

The direction of the electric field will depend on the values of σ₁ and σ₂. [see figure 2]

And at point P’ in region 3:

|E| = (σ₁ – σ₂)/(2ε₀) ………………….. (5)

The direction of the electric field will depend on the values of σ₁ and σ₂. [see figure 2]

Now let’s find out the electric field at P (in region 2, between 2 sheets)

At this point, the net electric field can be found as the sum of the electric field due to sheet 1 and the electric field due to sheet 2, because at these 2 points the directions of the electric field due to sheet 1 and the electric field due to sheet 2 are same.

And at point P in region 2:

|E| = (σ₁ + σ₂)/(2ε₀) …………………. (6)

The direction of the electric field is towards the right. [see figure 2]

Electric field due to two infinite plane charged conductors of finite thickness (both conductors charged with positive charge)

A plane charged conductor has a finite thickness, hence different charges show up on its two sides.

At point P’ in region 1:

|E| = (σ₁ + σ₂)/(ε₀) ……………. (7)

The direction of the electric field is towards the left. [see figure 3]

And at point P’ in region 3:

|E| = (σ₁ + σ₂)/(ε₀) ………….. (8)

The direction of the electric field is towards the right. [see figure 3]

Now let’s find out the electric field at P (in region 2, between 2 sheets of positive charges)

At this point, the net electric field can be found as the difference between the electric field due to sheet 1 and the electric field due to sheet 2, because at these 2 points the directions of the electric field due to sheet 1 and the electric field due to sheet 2 are opposite.

And at point P in region 2:

|E| = (σ₁ – σ₂)/(ε₀) ……………. (9)

The direction of the electric field will depend on the values of σ₁ and σ₂.

Electric field due to two infinite plane charged conductors of finite thickness (oppositely charged conductors)

Please note that a plane charged conductor has a finite thickness, hence different charges show up on its two sides.

At point P’ in region 1:

|E| = (σ₁ – σ₂)/(ε₀) ……………… (10)

The direction of the electric field will depend on the values of σ₁ and σ₂. [see figure 4]

And at point P’ in region 3:

|E| = (σ₁ – σ₂)/(ε₀) ………………….. (11)

The direction of the electric field will depend on the values of σ₁ and σ₂. [see figure 4]

Now let’s find out the electric field at P (in region 2, between 2 sheets)

At this point, the net electric field can be found as the sum of the electric field due to sheet 1 and the electric field due to sheet 2, because at these 2 points the directions of the electric field due to sheet 1 and the electric field due to sheet 2 are same.

And at point P in region 2:

|E| = (σ₁ + σ₂)/(ε₀) …………………. (12)

The direction of the electric field is towards the right. [see figure 4]