Electric Field due to a Plane Sheet of Charge
Last updated on May 11th, 2022 at 08:55 am
Electric Field due to a thin infinite Plane Sheet of Charge
In this section, we will derive the equation for the Electric Field due to a thin infinite Plane Sheet of Charge.
Consider a thin infinite plane sheet of charge ABCD, charged uniformly with surface charge density σ.
Note that, in a thin infinite plane sheet of charge, the same charge shows up on its two sides.
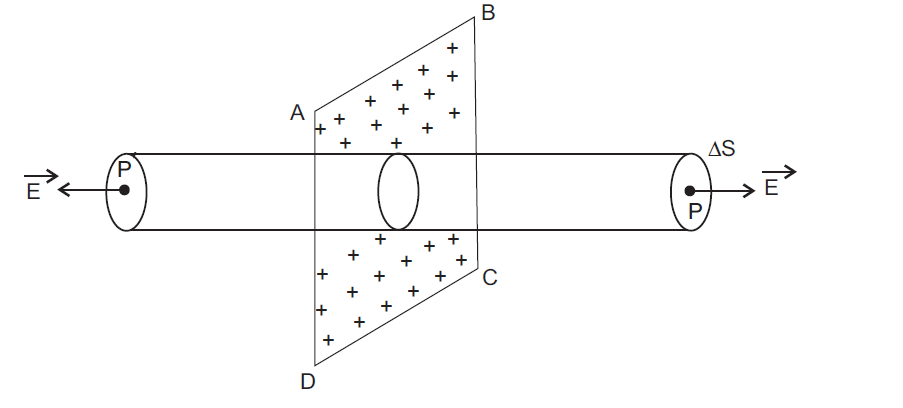
For symmetry reasons, the electric field will be perpendicular to the sheet (for both sides of the sheet), directed away from it, if σ > 0.
Let P be the point in front of the sheet where we want to find the electric field.
Draw a Gaussian surface in the form of a cylinder with its axis parallel to the field and one of its circular caps passing through P.
The other circular cap of the cylinder lies symmetrically opposite at P′, on the other side of the sheet, being situated at the same distance as P.
The electric flux through both the circular caps is
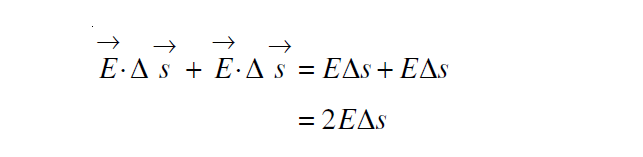
Note: for both sides of the surface the electric field will be perpendicular to the sheet. That means the surface vector Δs (perpendicular to the surface) and the Electric field E are parallel to each other. Hence, the angle between them = θ =0. Thus, cos θ = cos 0 = 1, for both the dot products in the previous line.
The electric flux through the curved surface of the Gaussian surface is
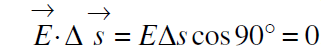
[θ =the angle between the electric field E and the surface vector Δs (which is perpendicular to the curved surface) is 90 degrees]
Hence, the total electric flux through the Gaussian cylinder is:
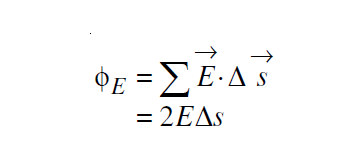
As the charge enclosed by the Gaussian cylinder is σΔs, using Gauss’ Law we have
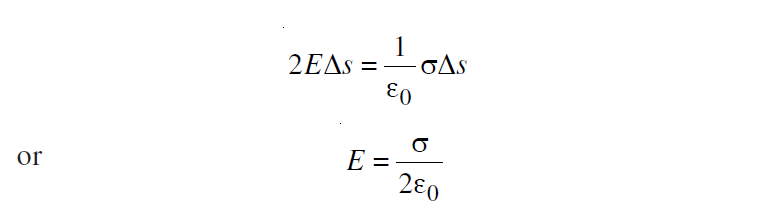
E =σ/2ε0
Please note that the electric field is independent of the distance from the sheet.
Note: as the infinite plane sheet is nonconducting and thin, we have considered only a single-sided charge distribution on the sheet to calculate the total charge and hence multiplied σ with Δs. As said above in the beginning, in this kind of sheet of charge, the same charge shows up on its 2 sides.
Electric field due to an infinite plane conductor having a finite thickness
Unlike the first scenario in this post, the infinite plane we discuss here is made of a conducting material having a finite thickness.
In this case, while deriving the expression of the electric field we need to consider a Gaussian surface that will contain charge on both sides of the conductor. Hence, the total charge included by the Gaussian surface = σ 2Δs. [ σ Δs on each side of the conductor]
Therefore, in such a case,
E 2Δs = σ 2Δs /ε0
=> E =σ/ε0
Summary
Electric Field due to a thin infinite Plane Sheet of Charge E =σ/2ε0
Electric field due to an infinite plane conductor having a finite thickness E =σ/ε0
