Capacitance of a Spherical Conductor (with formula derivation)
In this post, we will discuss and derive the formula of the Capacitance of a Spherical Conductor.
derivation of the Capacitance of a Spherical Conductor
Suppose an isolated spherical conductor of radius a metre is placed in a vacuum (or air). Suppose a charge of +Q coulomb is given to the sphere.
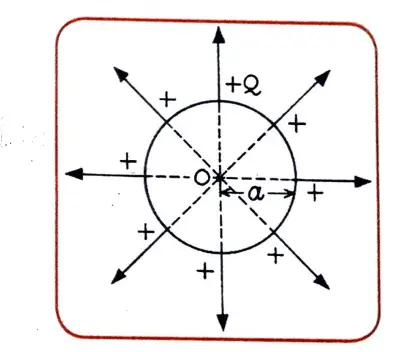
The capacitance of an Isolated Spherical Conductor
The charge spreads on the outer surface of the sphere uniformly so that the potential at every point on the surface is the same.
As a result, the lines of force emerging from the sphere are everywhere normal to the surface, that is, they appear to diverge radially from the centre O of the sphere.
Therefore, we can assume the charge +Q is concentrated at the centre O of the sphere. Then the potential at the surface of the sphere is
V = (1/4πε0) (Q/a) volt, where (1/4πε0) = 9×109 Nm2C-2 ………… (1)
If the capacitance of the sphere is C, then Q=CV
=> V =Q/C …………….. (2)
From equations (1) and (2) we get,
(1/4πε0) (Q/a) = Q/C
=> C = 4πε0a [the formula of the Capacitance of a Spherical Conductor – derived]
formula analysis
Thus the Capacitance of an Isolated Spherical Conductor is directly proportional to its radius.
The larger the radius, the greater the ability to hold charges.
ε0 is the permittivity of the free space or vacuum.
