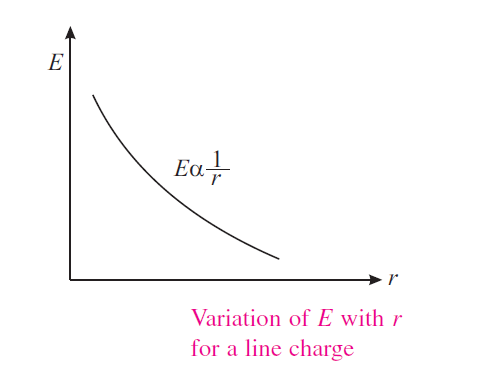Electric Field due to a Long Line Charge – formula derivation

Last updated on May 13th, 2022 at 05:10 am

A line charge is in the form of a thin charged wire of infinite length with a uniform linear charge density σ (charge per unit length). Let there be a charge +q on the wire.

We have to calculate the electric field at a point P at a distance r.

Draw a right circular cylinder of radius r with the long wire as the axis of the cylinder.

The cylinder is closed at both ends. The surface of this cylinder is the gaussian surface and is shown in Fig. 1. The magnitude of the electric field E is the same at every point on the curved surface of the cylinder because all points are at the same distance from the charged wire.

The electric field direction and the normal to area element Δs are parallel.

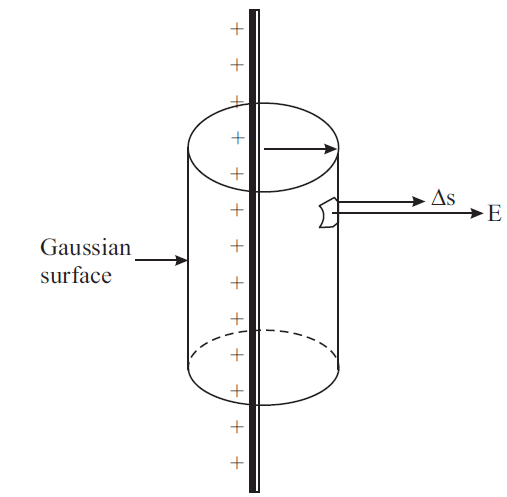
Let the length of the Gaussian cylinder be l. The total charge enclosed in the cylinder is q = σ l. The area of the curved surface of the cylinder is 2 πrl.
For the flat surfaces at the top and bottom of the cylinder, the normals to these areas are perpendicular to the electric field (cos 90° = 0). These surfaces, therefore, do not contribute to the total flux. Hence

φ_E = Σ E. Δs
= E × 2 πrl

According to Gauss’ law, φ_E = q/ε₀. Hence

E × 2 πrl = q/ε₀

=> E × 2 πrl = ƛ l/ε₀ [ Here, q = ƛl where ƛ = charge per unit length]

or E = ƛ l/(ε₀ 2 πrl ) = ƛ /(2 πε₀r )

E = ƛ /(2 πε₀r ) where ƛ = charge per unit length, and r = distance of the test point from the line of charge
(Electric Field due to a Long Line Charge at a distance r : formula derivation)

This shows that the electric field varies inversely with distance. (figure 2)