Atwood machine when pulley has a non-zero mass
In this post, we will analyze one Atwood machine when its pulley has a non-zero mass. As a result this pulley has a nonzero moment of inertia.
when pulley has a non-zero mass and nonzero moment of inertia
We will discuss the operation of an Atwood machine with a pulley that has a non-zero mass and nonzero moment of inertia.
Consider two masses hanging from a frictionless pulley with radius 𝑅 and mass 𝑀, as shown. Such a configuration is known as an Atwood machine. We have to find out the acceleration of the masses and the tensions in the string.
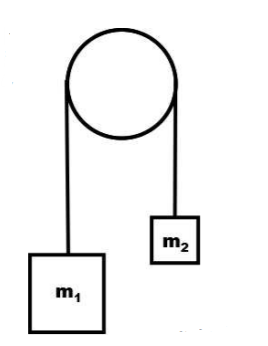
The first thing to realize is:
When the pulley in such a system has nonzero mass the tension in the string is no longer constant. It is easy to see why. If the pulley has mass 𝑀 it also has a nonzero moment of inertia 𝐼 = (1/2) 𝑀𝑅2.
As the masses accelerate, the pulley undergoes an angular acceleration 𝛼, and so by Eq. (T = I α) the torque 𝜏 must be nonzero.
Because the string is the only thing producing the torque and acts at right angles to the axle, Eq. (T = F x r) tells us that the total torque is 𝜏 = (𝑇𝐿 − 𝑇𝑅)𝑅, where the radius 𝑅 of the pulley is the lever arm and 𝑇𝐿 and 𝑇𝑅 are the tensions on the left and right sides of the pulley, respectively.
If 𝑇𝐿 and 𝑇𝑅 were the same, the torque would be zero; since the torque cannot be zero, the tensions must be unequal.
In solving this problem, it may help to visualize the masses stretched out in a line, with gravity pulling 𝑚1 to the left and 𝑚2 to the right. 𝑇𝑅 then acts to the left and 𝑇𝐿 acts to the right.
Call to the left positive. Newton’s 2nd law for 𝑚1 becomes:
𝑚1𝑎1 = 𝑚1𝑔 − 𝑇L
Newton’s 2nd law for 𝑚2 is:
𝑚2𝑎2 = −𝑚2𝑔 + 𝑇R
However, the string provides a physical constraint that requires 𝑎2 = 𝑎1. Call the joint acceleration 𝑎. Then
adding the two equations gives
(𝑚1 + 𝑚2)𝑎 = (𝑚1 − 𝑚2)𝑔 + 𝑇𝑅 − 𝑇L
We know from above that 𝜏 = (𝑇𝐿 − 𝑇𝑅)𝑅 = 𝐼𝛼 = (1/2) 𝑀𝑅2𝛼. If the string does not slip on the pulley we can say that 𝛼 = 𝑎/𝑅
Then 𝑇𝐿 − 𝑇𝑅 = (1/2) 𝑀𝑎 and
𝑎 =(𝑚1 − 𝑚2)g/[m1 + m2 + M/2]
If 𝑚1 = 𝑚2, then 𝑎 = 0, as expected since the force of gravity is acting on the two masses equally.
Further, 𝑎 is less when 𝑀 ≠ 0 than when 𝑀 = 0; with a nonzero 𝐼, the pulley has inertia and adds an effective mass to the system, lessening any acceleration.
One can now find the tensions by merely plugging the expression for 𝑎 back into the top two equations.
