Center of Mass of a system and its velocity – definition & equation

In this post, we will discuss the Center of Mass and its Momentum & velocity.

---

Center of mass – for a single object & for collection of masses

The center of mass (CM) is closely related to the concept of momentum. In most of the discussions and numerical problems, we assume that the various objects behave like point particles whose entire masses are concentrated at their centers.

For a single, symmetrical object, such as a block or billiard ball, the center of the object is the center of mass. Hence, all the velocities and accelerations that we often refer to are those of the CM of the moving objects.

For a collection of masses, the situation is more complex. You know that to balance a seesaw, the heavier person must sit closer to the fulcrum than the lighter person. The balance point or the position of the fulcrum is the center of mass of the system. In other words, in a balanced seesaw, the position of the fulcrum is the center of mass of the system

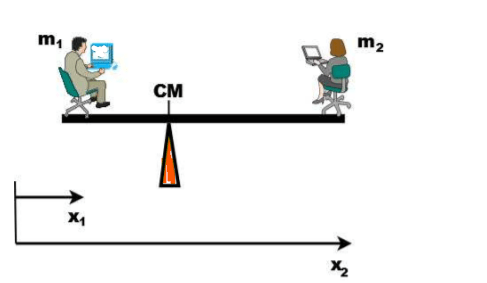
Center of mass – definition & formula

Mathematically, the position of the center of mass is defined as the “average” position of all the objects measured from any convenient origin:

x_CM = (m₁x₁ + m₂x₂ + m₃x₃ + …. + m_nx_n) / (m₁ +m₂ + m₃ + … + m_n) …………(1)

where the denominator is 𝑀_𝑡𝑜𝑡, the system’s total mass.

For example, if you place the origin at the fulcrum, then 𝑥_𝐶𝑀 = 0, and if there are two people of equal mass sitting on the seesaw, then Equation (1) gives:
0 = m 𝑥₁ + m 𝑥₂
=> 𝑥₁ = −𝑥₂

Velocity of the system’s center-of-mass & its equation

Now, Equation (1) implies that the velocity of the system’s center-of-mass must be:

v_CM= (m₁v₁ + m₂v₂ + m₃v₃ + …. + m_nv_n) / (m₁ +m₂ + m₃ + … + m_n) …………(2)

But the numerator is just the sum of all the momenta of the objects: 𝑝₁ + 𝑝₂ + ⋯ + 𝑝_𝑛. If the system is isolated, we know that its total momentum cannot change. The denominator is 𝑀_𝑡𝑜𝑡, the system’s total mass.

Equation (2) then immediately implies that the velocity of the center of mass of an isolated system remains constant. In particular, if the center of mass of an isolated system is initially at rest, it remains at rest for eternity.

Summary | Take away

1 ) Mathematically, the position of the center of mass is defined as the “average” position of all the objects measured from any convenient origin

2 ) The velocity of the center of mass of an isolated system remains constant.

3 ) In particular, if the center of mass of an isolated system is initially at rest, it remains at rest for eternity.