Potential Energy Diagrams of different types

In this post, we will draw different types of Potential Energy Diagrams. Each of these diagrams is based on a specific equation of potential energy.

For elementary courses and the College Board exams, the most important types of potential energy are gravitational potential energy and spring potential energy, also known as “harmonic oscillator potential energy.”

Potential Energy Equations

1 ) 𝐺𝑟𝑎𝑣𝑖𝑡𝑎𝑡𝑖𝑜𝑛𝑎𝑙 𝑃𝑜𝑡𝑒𝑛𝑡𝑖𝑎𝑙 𝐸𝑛𝑒𝑟𝑔𝑦 = 𝑈_𝑔 = −𝐺𝑚₁𝑚₂/r, Here 𝑟 is the distance between the centers of two spherical bodies.

2 ) Potential energy due to the position of mass 𝑚 at a height ℎ above the earth’s surface can be expressed as 𝑈_𝑔 = mgh. Here, h<< Radius of the earth.

3 ) The other form of potential energy that frequently arises in elementary physics, is that associated with a spring.
It is given by U_s = (1/2) k x². In this equation 𝑘 is the spring constant and 𝑥 = Δ𝑠 is the amount of stretch or extension.

---

Potential Energy Diagrams | PE Diagrams

Here are 3 different Potential energy diagrams. For better understanding, the corresponding PE equation is given for every PE diagram.

Potential Energy Diagram for 𝐺𝑟𝑎𝑣𝑖𝑡𝑎𝑡𝑖𝑜𝑛𝑎𝑙 𝑃𝑜𝑡𝑒𝑛𝑡𝑖𝑎𝑙 𝐸𝑛𝑒𝑟𝑔𝑦 𝑈_𝑔 = −𝐺𝑚₁𝑚₂/r

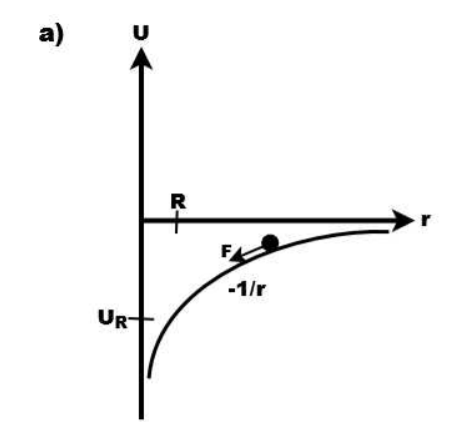
figure 1(a) shows the gravitational potential energy Equation 𝑈_𝑔 = −𝐺𝑚₁𝑚₂/r
It follows a 1/𝑟 curve and one immediately sees that 𝑈 → 0 as 𝑟 → ∞ and that 𝑈 → −∞ as 𝑟 → 0. The radius of, for example, the Earth 𝑅 is indicated as well as the potential 𝑈_𝑅 at that point, which is negative.

Potential Energy Diagram for 𝑃𝑜𝑡𝑒𝑛𝑡𝑖𝑎𝑙 𝐸𝑛𝑒𝑟𝑔𝑦 𝑈_𝑔 = mgh

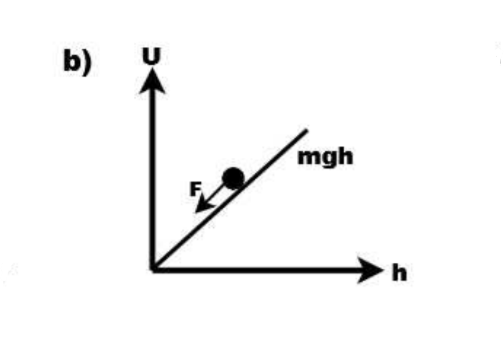
Figure (b) is the approximation to the potential shown in figure 1(a) in the vicinity of 𝑅. 𝑈_𝑅 is taken to be zero at the point ℎ = 𝑅 (at the earth’s surface) and the potential above that point is approximated as a straight line.

Potential energy diagram for spring potential energy U_s = (1/2) k x²

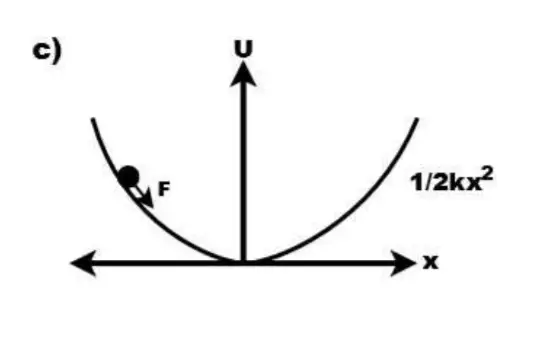
Figure (c) shows the spring, or harmonic oscillator, potential. Since the equation for this potential energy is U_s = (1/2) k x², the shape of the diagram is that of a parabola.