Simple Harmonic Motion of a Simple Pendulum
In this post, we will focus on a specific example of Simple Harmonic motion and it is the Simple Harmonic Motion of a Simple Pendulum.
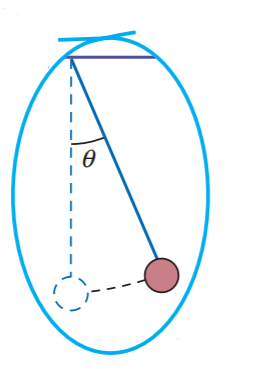
A simple pendulum consists of a mass called a bob, which is attached to a fixed string, as shown in Figure 1. When working with a simple pendulum, we assume that the mass of the bob is concentrated at a point and that the mass of the string is negligible. Furthermore, we disregard the effects of friction and air resistance.
For a physical pendulum, on the other hand, the distribution of the mass must be considered, and friction and air resistance also must be taken into account.
To simplify our analysis, we will disregard these complications and use a simple pendulum to approximate a physical pendulum in all of our examples.
The restoring force of a pendulum is a component of the bob’s weight
To see whether the pendulum’s motion is simple harmonic, we must first examine the forces exerted on the pendulum’s bob to determine which force acts as the restoring force.
If the restoring force is proportional to the displacement, then the pendulum’s motion is simple harmonic.
Let us select a coordinate system in which the x-axis is tangent to the direction of motion and the y-axis is perpendicular to the direction of motion. Because the bob is always changing its position, these axes will change at each point of the bob’s motion.
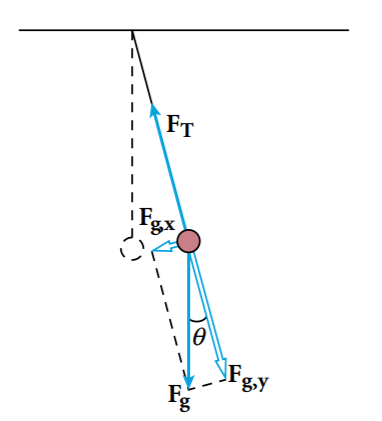
The forces acting on the bob at any point include the force exerted by the string and the gravitational force. The force exerted by the string always acts along the y-axis, which is along the string. The gravitational force can be resolved into two components along the chosen axes, as shown in Figure 2.
be resolved into two components.
Because both the force exerted by the string and the y component of the gravitational force are perpendicular to the bob’s motion, the x component of the gravitational force is the net force acting on the bob in the direction of its motion.
In this case, the x component of the gravitational force always pulls the bob toward its equilibrium position and hence is the restoring force. This x component (Fg,x) is perpendicular to the string and it is the only force acting on the bob in the direction of its motion.
Note that this restoring force (Fg,x = Fg sin θ) is zero at equilibrium because θ equals zero at this point.
For small angles, the pendulum’s motion is simple harmonic
The restoring force of a simple pendulum is not constant. Instead, the magnitude of the restoring force varies with the bob’s distance from the equilibrium position.
The magnitude of the restoring force is proportional to sin θ. When the maximum angle of displacement θ is relatively small (<15°), sin θ is approximately equal to θ in radians. As a result, the restoring force is very nearly proportional to the displacement and the pendulum’s motion is an excellent approximation of simple harmonic motion.
We will assume small angles of displacement unless otherwise noted.
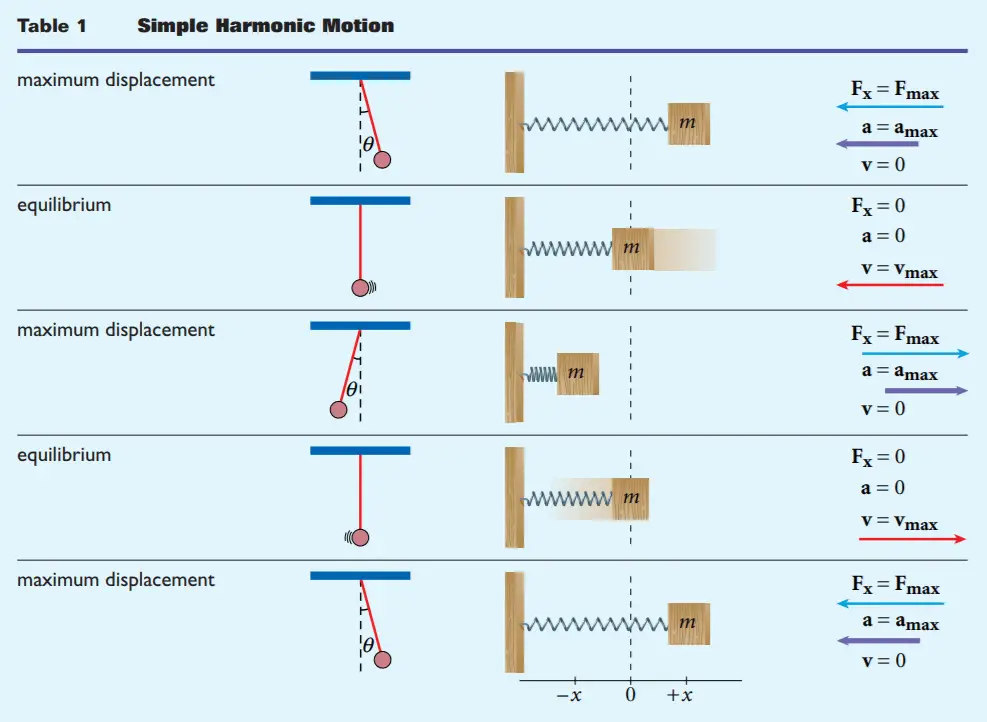
- At maximum displacement, the restoring force and acceleration reach a maximum while the speed becomes zero.
- Conversely, at equilibrium, the restoring force and acceleration become zero and speed reaches a maximum.
the analogy between a simple pendulum and a mass-spring system
The graphic table below shows the analogy between a simple pendulum and a mass-spring system, as both of them undergo simple harmonic motion. For both the systems the following are true: