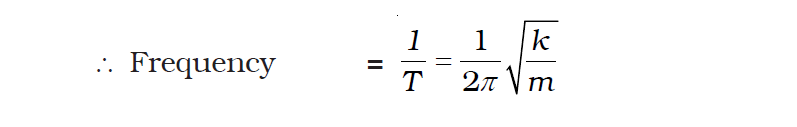Harmonic Motion of a mass attached to a Spring with Horizontal oscillations – with graph | Time period equation & frequency

Last updated on April 12th, 2021 at 04:38 am

Horizontal oscillations of spring cause the Harmonic Motion of a mass attached to the Spring. We will study this here with diagrams and graphs and find out the following: A mass attached to spring makes a harmonic motion – when and how this happens? When do we call a motion Harmonic?

So, Let’s try to find out the answers to these queries.

Just to brush up – we already covered the “spring force”, a force that is proportional to the displacement and opposes it.

As you will surely recall, the force from an “ideal” spring followed the formula given in Equation (1), F = −kx ………………… (1)
where k was called the “force constant” of the spring and x is the displacement of the end of the spring from the equilibrium position.

You’ll also recall that the energy stored in the spring is PE = (1/2)kx².

How a mass attached to a Spring gets into Harmonic Motion due to Horizontal oscillations of spring? – Explain with Graphs

To observe this motion, we’ll attach a mass m to the end of spring, pull the mass back a little way (a distance A), and then release it, as shown in Fig. (1). (The surface on which the mass is sliding is frictionless!)

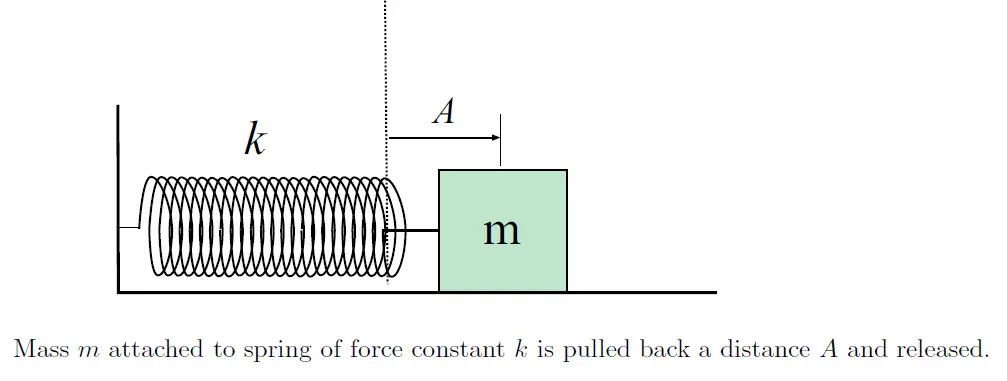
Since the mass gets pulled inward when the spring is stretched and gets pushed outward when the spring is compressed we expect the motion to be represented by something like the x vs. t graph in Fig. (2).

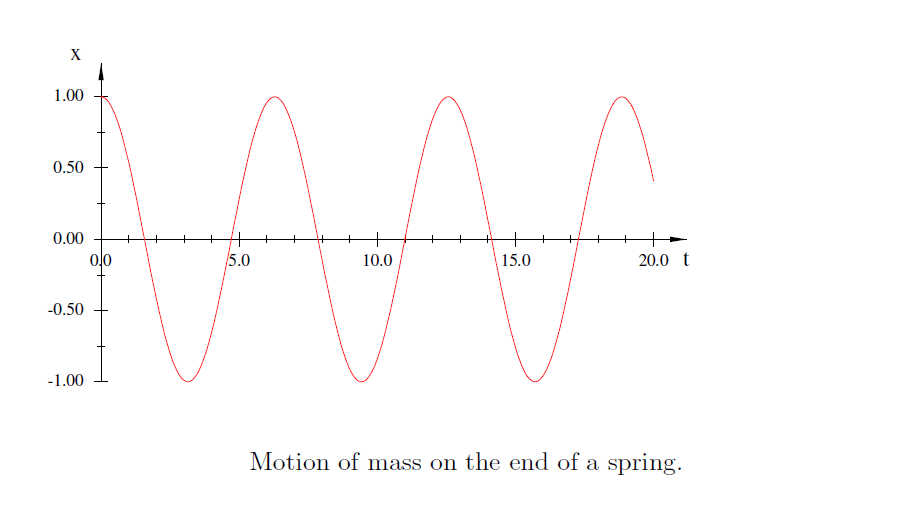
The graph in Fig. (2) shows how the mass would move if the spring is ideal and obeys the force law F = −kx.

The curve is “sinusoidal” meaning that it follows the basic form of the sine or cosine functions seen in math.

When the motion of an object depends on time in this sinusoidal fashion, we say that the object is undergoing harmonic motion and that the physical system producing such a motion is a harmonic oscillator.

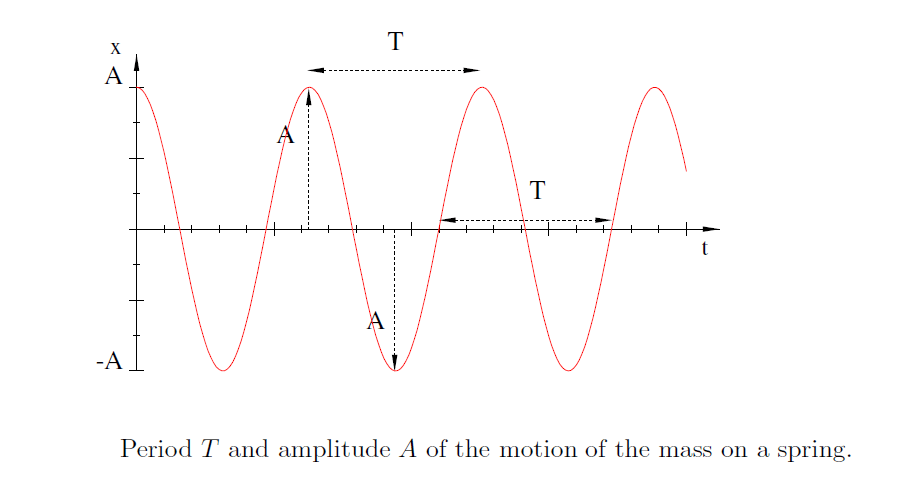
The maximum distance which the mass goes outward from the equilibrium point is the same as the maximum distance it goes inward. This distance is called the amplitude of the motion. In Fig. (3) the amplitude is indicated by A. (For the mass’s motion the amplitude is a length and is measured in meters.)

Frequency and Time Period of the Mass having harmonic motion due to Horizontal oscillations of the attached spring

Then there is the amount of time required for the mass to make one full oscillation, that is, to go back and forth and return to a place where its motion will repeat itself. This is the period of motion, and it is indicated (twice) in Fig. 3. The period T is a time and is measured in seconds.

A related number describing the rapidity of the oscillations is the number of oscillations the mass will make in a given time period(per unit time); this is called the frequency of the oscillations:
f =(number of oscillations)/time …. (2)

The frequency is the number of oscillations per unit time, but the time for each oscillation is the period T so that f is the inverse of T:
=> f =1/T
or, T = 1/f

What is the equation of time period for the spring-mass system with horizontal oscillation?

The time period equation is stated as follows: T = 2π √(m/k)

Derivation of the equation of time period for the spring-mass system with horizontal oscillation

Restoring force F = −kx.
From Newton’s second law, we know that F = ma
∴ ma = −kx
a =−kx/m

Comparing with the equation of SHM a = −ω²x, we get

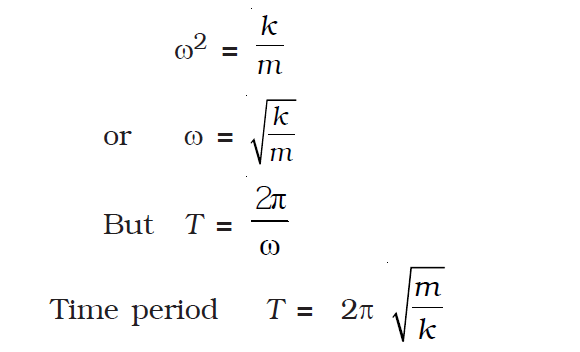
Thus, we can quickly derive the equation of time period for the spring-mass system with horizontal oscillation.

Equation of frequency for the spring-mass system with horizontal oscillation – derivation

Equation of Frequency can be stated as f = [1/(2π)]√(k/m)

And, this is how we get it from the equation of time period: