velocity of the pendulum bob at the equilibrium position

In this post, we will derive an equation for the velocity of the pendulum bob at the equilibrium position.

Calculating the velocity of the pendulum bob at the equilibrium position requires that we arrange our coordinate system so that the height of the bob at the equilibrium position is zero.

Then the total mechanical energy is equal to the kinetic energy at the equilibrium point where Potential energy (U) = 0.

The total mechanical energy is also equal to the total potential energy at θ_max where KE = 0.

Putting these conditions together, we get

E = (1/2)mV²=mgh …………………. (1)

Now, we have to find out the expression of h. For this, we will refer to figure 1.

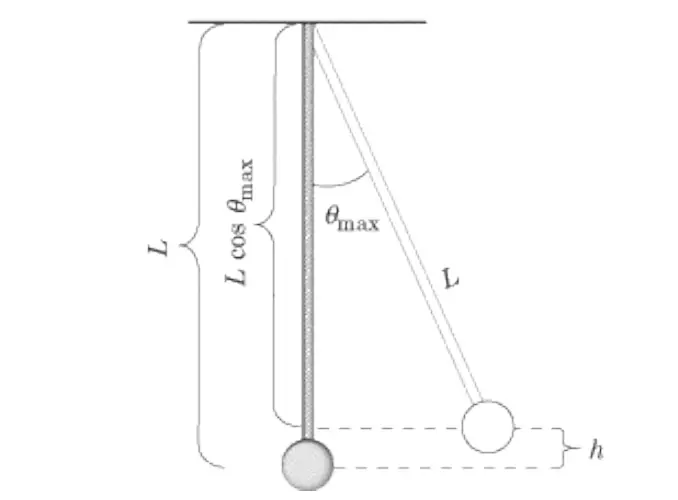
From the figure, we see that h=L – L cos θ_max ………….. (2)

If we plug that value into equation 1 above, we can solve for v:

(1/2)mv² = mg (L – L cos θ_max )

v = [2gL(1-cos θ_max)]^1/2

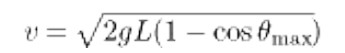
What we get from this equation of pendulum bob velocity at the equilibrium is:

• The longer the string the faster the pendulum bob will move.
• The greater the angle, the faster the pendulum bob will move.