Transfers between kinetic & potential energy in a simple pendulum
Last updated on November 12th, 2021 at 04:38 am
In this post, we will discuss how transfers between kinetic energy and potential energy happen in a simple pendulum. We will also discuss Energy Conservation in a Simple Pendulum. Finally, we will derive the equation for the maximum speed of the pendulum bob.
How Transfer between KE and PE happens in a simple pendulum?
A simple pendulum is an excellent approximation of an isolated system.
During its downswing, Earth’s gravity does work on the pendulum to transfer gravitational potential energy into kinetic energy. On the upswing, gravity transfers kinetic energy back into gravitational potential energy. The mechanical energy of the pendulum is constant.
At the lowest point of the pendulum’s swing, the gravitational potential energy would be zero and the mechanical energy would be equal to the kinetic energy. Then, at the highest point on the swing, where movement stops and kinetic energy is zero, the mechanical energy would be equal to the potential energy.
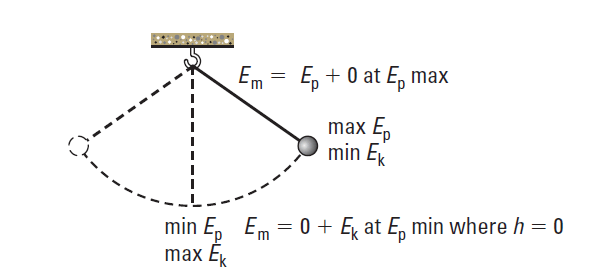
To calculate the mechanical energy of a pendulum it is necessary to know its mass, its height above the reference point, and its speed. If all of those values are known at any one point on its swing, then the mechanical energy of the pendulum is known at all points on its swing. Once the mechanical energy is known, it can be used to predict the pendulum’s motion at any instant along its path and to correlate kinetic and potential energy with the amplitude of the swing.
Energy Conservation in a Simple Pendulum
As a pendulum swings, gravity acts to convert energy back and forth between gravitational potential energy and kinetic energy.
During its downswing, Earth’s gravity does work on the pendulum to transfer gravitational potential energy into kinetic energy. On the upswing, gravity transfers kinetic energy back into gravitational potential energy. The mechanical energy of the pendulum is constant.
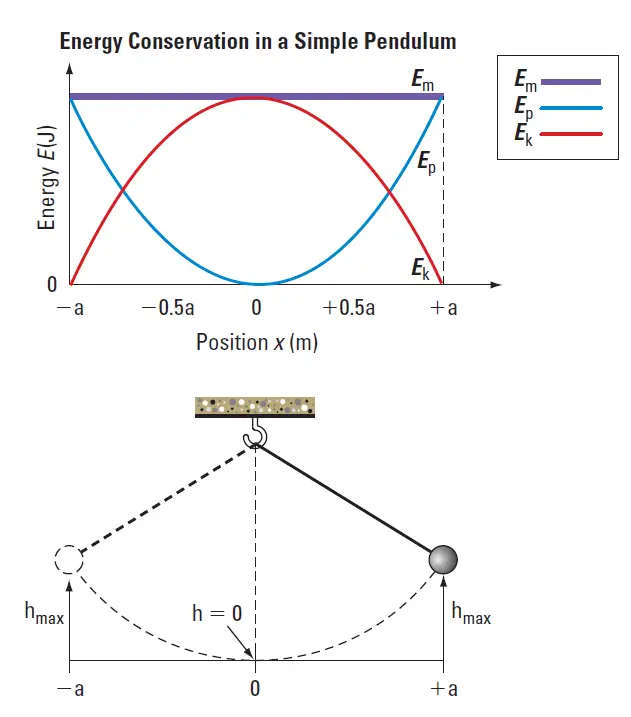
mechanical energy remains constant.
Deriving The maximum speed of the pendulum bob
let’s consider the diagram of a simple pendulum below to find out how transfer between KE and PE happens in a simple pendulum:
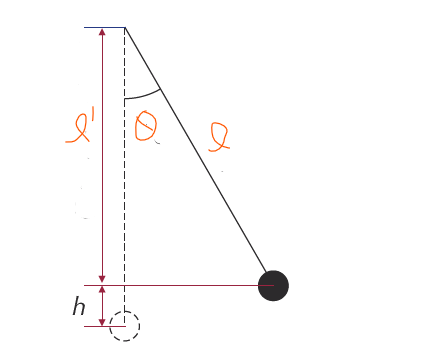
Let’s consider a simple pendulum that has a mass of m and a length of l.
Say, It is pulled out to an angle of θ° from the vertical.
We will first find the gravitational potential energy stored in the pendulum bob relative to its lowest point.
As you can see as the pendulum is pulled out its height has increased by h.
And, you can work out the increase in height, h, of the end of the pendulum using trigonometry.
As per figure 1, we can write the following equations:
l’= l cos θ …….. (1)
h + l’ = l …….. (2)
=> h = l – l’
=> h = l – l cos θ …………. (3)
So the gravitational potential energy of the pendulum as it is pulled out to the height h can be found in this way:
PE = m g h = mg ( l – l cos θ ) ………… (4)
Then the pendulum is released from height h. We have to find the maximum speed v of the pendulum bob as it passes through the vertical position.
To find the maximum speed, assuming no air resistance, we will use this equation (1/2)mv2 = mgh
=> (1/2)mv2 = mg ( l – l cos θ ) ………. (5)
Hence, the maximum speed of the pendulum bob is derived as v = √[2g ( l – l cos θ )]

