The effect of air resistance on projectile motion

Last updated on February 8th, 2024 at 10:37 am

In this post, we will find the effect of air resistance on projectile motion. We have seen that in the absence of air resistance, the trajectory or path followed by a projectile is a parabola and that the path depends only on the initial speed and angle of projection. But in the real world, all projectiles are subject to air resistance. Hence in this post, we will analyze the projectile motion subjected to air resistance.

Fig 1 shows the free-body force diagram for a projectile subject to air resistance.

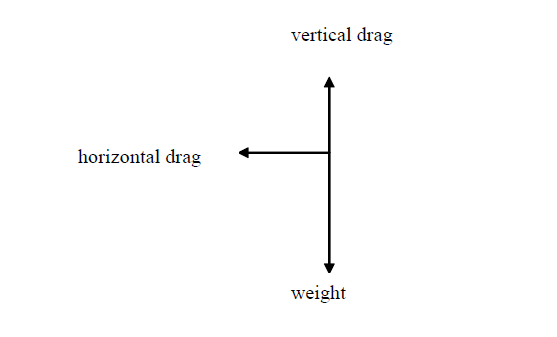
When air resistance is not considered, weight is the only force acting vertically on the projectile, but as air resistance comes into the picture, vertical drag also acts on the projectile as a vertical force. When air resistance is not considered, there is no horizontal external force on the projectile. But, as air drag is considered we get a horizontal drag force as well acting on the projectile in the horizontal direction.

Experiment shows that both the horizontal and vertical drag forces depend on the speed of the projectile.

The effect of the horizontal air drag will be to foreshorten the range of the projectile and the effect of the vertical air drag will be to reduce the maximum height reached by the projectile.

However, the presence of air resistance also means that the mass of the projectile will now affect the path followed by the projectile.

In the absence of air resistance, there is no acceleration in the horizontal direction and the acceleration in the vertical direction is g,
the acceleration of free fall.

With air resistance present, to find the horizontal (a_H) and vertical (a_V) accelerations we have to apply Newton’s second law to both directions.

If we let the horizontal drag equal K₁V_H and the vertical drag equal K₂V_v where K₁ and K₂ are constants and V_H and V_v are the horizontal and vertical speeds respectively at any instant, then we can write

K₁V_H = m a_H …………… (1)

mg – K₂V_v = m a_V ………..(2)

From this, we can now see why the mass affects the path of the projectile when air resistance is considered.

Both horizontal acceleration (a_H) and vertical (a_V) acceleration are found to be dependent on the mass m of the projectile if air resistance is present.