Horizontal projectiles – formulas with derivation

Horizontal projectiles are directed straight out as a horizontal projection. It undergoes downward acceleration under the influence of gravity and hence gets an increasing downward velocity. At the same time, the horizontal velocity of the horizontal projectile remains the same throughout the flight as there are no forces in the horizontal direction if you ignore air resistance. The combination of the increasing vertical (Vv) motion and the unchanging horizontal (Vh) motion causes this type of projectile to follow a curved path until it hits the ground.

We have already discussed and made the derivation of projectile motion equations for projectiles directed at some angle between the vertical and the horizontal. Here we will discuss and derive projectile motion equations for horizontally launched projectiles only.

Deriving equations of the horizontal projectile

To derive the equations for horizontal projectiles we will refer to the following figure:

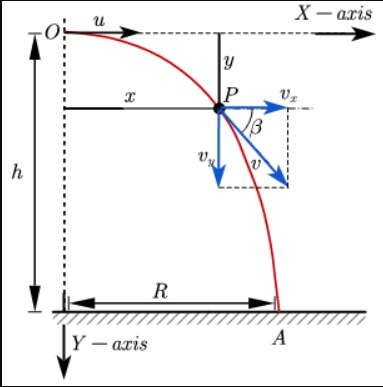
Suppose a body is thrown horizontally from a point O with velocity u. h is the height of Point O with respect to the ground.

Now the body moves along path OPA under the influence of two simultaneously independent motions listed below:
(i) motion with uniform horizontal velocity u.
(ii) vertically downward accelerated motion with constant acceleration g (due to gravity).

In this figure Y-axis is taken downwards, therefore, the downward direction will be regarded as the positive direction. So in the equations, we will refer to the downward acceleration ay of the projectile as +g.

Trajectory equation of the horizontal projectile & its derivation

Say, after a time duration of t the projectile reaches point P (x,y).

Considering motion with uniform velocity along X-axis, distance traveled along the X-axis in time t can be expressed as:

x = u t

hence, t = x/u .…….……. (1)
Now, Considering motion along Y axis,

u_y = 0 (initial velocity along Y axis, at t = 0)
a_y = g

Now, distance traveled along the Y-axis can be expressed as:
y = u_y t + (½) g t²
=> y = (½) g t² ……………… (2)

From 1 & 2 we get,
y = (½) g t²
=> y = (½) g (x/u)²
=> y = [g/(2u²)] x²

This is the equation of a parabola.
So, the trajectory of the projectile launched parallel to the horizontal is a parabola.

The velocity equation of the horizontal projectile | derive the equation of horizontal projectile velocity

Along the horizontal axis,a_x =0
so, velocity remains constant along horizontal axis.
So at point P, v_x = u ……………… (i)

Considering motion along vertical axis,
v_y = u_y + g t
As, initial velocity along Y axis = u_y = 0,
hence, v_y = g t …………(ii)
Magnitude of resultant velocity at any point P
v² = v_x² + v_y²
=> So the equation of the horizontal projectile velocity is:
v = √(v_x² + v_y²) = √(u² + g² t²) …………….. (3)

Now if β is the angle which resultant velocity makes with the horizontal, then
tanβ = v_y/v_x= gt / u
=> β = tan^-1(gt/u)

Time of flight of a projectile launched horizontally

It is the total time for which the projectile remains in flight (from O to A). Let T be the time of flight.
For the vertical downward movement of the body we use this equation:
s_y = u_y + (½) g t²

=> h = 0 + (½) g T²

Time of flight of a horizontal projectile = T = √(2h/g) …………… (4)

Range of a horizontal projectile

It is the horizontal distance covered by the projectile during the time of flight. It is equal to OA = R.
Here we will use the equation for the time of flight, i.e. equation (4) above.

So, R=Horizontal velocity×Time of flight=u×T=u√(2h/g)

Hence, Range of a horizontal projectile = R = u√(2h/g)

---

Velocity with which the projectile hits the ground :

At A, v = √(v_x² + v_y²)

At A,
v_x=u….. (i)
v_y² = 0 + 2gh
v_y=√(2gh) …(ii)

Hence, v = √(v_x² + v_y²) = √(u² + 2gh)
So, the Velocity with which the projectile hits the ground (v) = √(u² + 2gh)