Projectile Motion Formulas in a List
Last updated on May 16th, 2023 at 10:07 am
In the next section, we will list down the Projectile Motion Formulas or equations. (Projectile trajectory equation & other formulas like maximum height and horizontal range of the projectile, time of flight, etc.)
On another page on this site, Find the derivation of Projectile equations – parabolic path, max height, range, & time of flight.
Projectile motion formula list
Projectile motion is the motion of a projected object in flight which is a result of two separate simultaneously occurring components of motion. One component of motion is without any acceleration along a horizontal direction and the other is along the vertical direction with constant acceleration due to the force of gravity (considering air resistance as negligible).
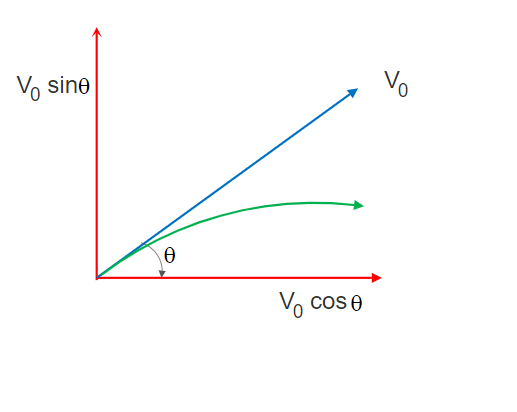
The initial velocity component along X-axis = V0x = V0 cosθ and the initial velocity component along Y-axis = V0y = V0sinθ.
(Air resistance is taken as negligible). g is the acceleration due to gravity.
| Initial Horizontal Velocity | V0x = V0 cosθ [along X axis] |
| Horizontal velocity | VX = V0x = V0 cosθ [ uniform horizontal velocity] |
| Initial Vertical velocity | V0y = V0sinθ [along Y axis] |
| Vertical velocity | Vy = V0sinθ – g t [ acceleration = -g] |
| Horizontal displacement | x= V0x.t = (V0 cosθ). t |
| Vertical displacement | y= (V0sinθ ).t – (1/2) g t2 |
| Motion Path equation (parabola equation): | y = (tanθ) x – (1/2) g . x2/(V0 cosθ)2 [Parabolic] |
| Time to reach max height: | tmax= (V0sinθ )/g |
| Total time of flight for a projectile | Ttot = 2(V0sinθ )/g |
| Maximum height reached: | Hmax = ( V0sinθ )2/(2 g) |
| Horizontal range of a projectile: | R = (V02 sin2θ )/ g |
| Maximum possible horizontal range: | Rmax = V02 / g |
Projectile Motion Solved Example
A ball is thrown at a speed of 28 m/s in a direction 30 degrees above the horizontal. Calculate (a) the maximum height (b) the time taken by the ball to return to the same level (c) the distance from the thrower to the point where the ball returns to the same level.
Solution:
V0 = 28 m/s, θ = 30 degrees
(a) The maximum height = Hmax = ( V0sinθ )2/(2 g) = (28 Sin 30)^2 / (2×9.8) m = 10 m
(b) the time taken by the ball to return to the same level = Total time = Ttot = 2(V0sinθ )/g = (2x28xsin 30) /9.8 = 2.9 s
(c) the distance from the thrower to the point where the ball returns to the same level = Horizontal range of a projectile = R = (V02 sin2θ )/ g = (28x28xsin 60)/9.8 =69 m
