Average velocity – definition, formula, numerical problem

Last updated on May 8th, 2021 at 09:55 am

How fast an object is moving can be expressed by the rate at which the position of the object changes with time. For each position x_i, we assign a particular time t_i. If the details of the motion at each instant are not important, the rate is usually expressed as the average velocity v.

Average Velocity is defined as a vector quantity that is simply the total displacement between two points divided by the time taken to travel between them. The time taken to travel between two points is called the elapsed time Δt.

Average Velocity Formula | How to find Average Velocity

If x1 and x2 are the positions of an object at times t1 and t2, respectively, then

Average velocity = v = Displacement between two points/Elapsed time between two points

v = Δx/Δt = (x2 − x1)/(t2 − t1) ……………….(1)

It is important to note that the average velocity is a vector and can be negative, depending on positions x1 and x2.

Numerical Problem on Average Velocity with solution

# problem with the solution
Q 1.] Rupa sets out from her home to meet her friends, traveling due east along her street. At 0.5 km and 9 minutes later she remembered something important and has to retrace her steps back to her house.

This takes an additional 9 minutes. After doing her job at home, she sets out again on the same path and ends up 1.0 km from her house. This third leg of her trip takes 15 minutes. At this point she turns back toward her house, heading west. After 1.75 km and 25 minutes, she stops to rest.

a. What is Rupa’s total displacement to the point where she stops to rest?

b. What is the magnitude of the final displacement?

c. What is the average velocity during her entire trip?

Q1] Solution:

The position towards the east is taken as positive (Positive x-axis) and towards the west, it’s taken as negative (Negative X-axis).

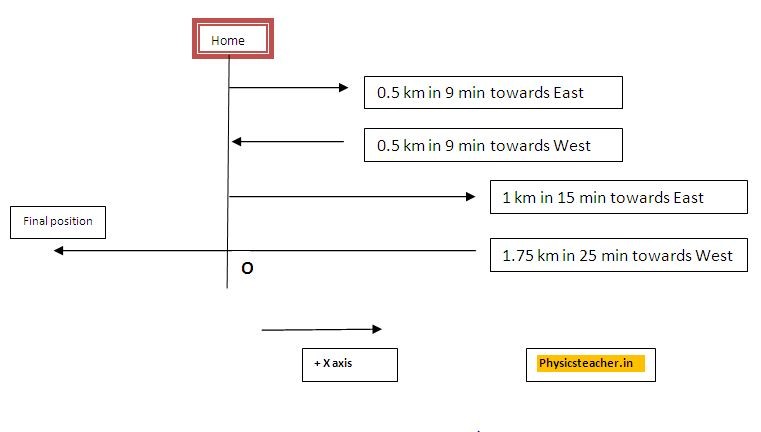
a) Total displacement = shortest distance between the final location and initial location =[ – 0.75 – 0 ] km= – 0.75 Km

b) Magnitude of final displacement = | -0.75| Km = 0.75 Km

c.
Total elapsed time = 9 + 9 + 15 + 25 = 58 min
The avg. velocity = Total displacement / Elapsed time = [-0.75]/[58] Km/min
= – 0.013 Km/min

In SI: The average velocity = [-0.75 * 1000]/[58 * 60] m/s = – 0.21 m/s

Problem Q2] The position of a particle is given by x(t) = 3.0t + 0.5t³ m .

a. Calculate the average velocity between 1.0 s and 3.0 s.

Solution: To determine the average velocity V of the particle between 1.0 s and 3.0 s, we calculate the values of x(1.0 s) and x(3.0 s):

x (1.0 s) = [ 3. 1 + 0.5. (1)³] m = 3.5 m

x (3.0 s) = [ 3. 3 + 0.5. (3)³] m = 22.5 m

Then the required V = [ x (3.0 s) – x (1.0 s) ] / [ t (3.0s) – t(1.0s)]
= (22.5 – 3.5)/(3-1) = 9.5 m/s

Also Read: (suggested reading)

Difference between Instantaneous Speed and Instantaneous Velocity

Difference between average speed and average velocity

Instantaneous Velocity – definition & equation with solved problem

Average velocity – definition, formula

Instantaneous Acceleration – definition & formula with solved problem

Average Acceleration and its formula & solved numerical problems