Simple Parallel circuit, Equivalent resistance in a parallel circuit with derivation & numerical problems

Last updated on April 20th, 2023 at 04:54 pm

In this post, we will study a simple parallel circuit. Then we will derive the equivalent resistance formula in a parallel circuit. Using this formula, we will solve numerical problems related to parallel circuits.

Simple Parallel circuit | Resistance in Parallel | Resistors in parallel

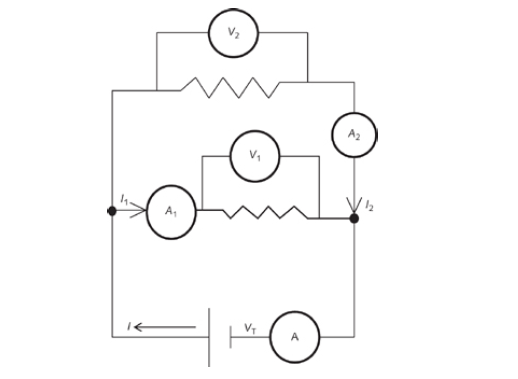
A simple parallel circuit is shown below. Three resistances (resistors) are in parallel in this circuit. The supply voltage is applied in parallel to these parallel resistors.

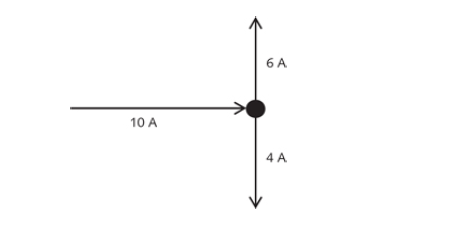
The equivalent resistance in a parallel circuit is found using Kirchoff’s junction rule, which states that the sum of the currents entering a branch (or junction) must be equal to the sum of the currents leaving a branch (or junction).

This is illustrated in Figure 2 (the black dot represents the branch point). See how 10 A current is entering the junction and again 6+4 =10 A current is coming out of it through two branches. The concept of a circuit branch is necessary to understand parallel circuits.

Derivation of the Equivalent resistance in a parallel circuit

A simple parallel circuit would look like Figure 3. The circuit current I splits into two currents, I1 and I2 (as measured by ammeters A1 and A2). Those two currents must add up to the total circuit current I coming from the battery.

However, experiments show that the potential drops across each resistor in parallel are the same.

Thus, we have a parallel circuit:
V_T = V₁ = V₂ = V₃ = ….. (a)
I = I₁ + I₂ + I₃ +… (b) [ current I gets distributed among parallel paths.]

Now, using Ohm’s Law in equation (b) we get,

V_T/R_eq = V₁/R₁ + V₂/R₂  + V₃/R₃ ..

=> V_T/R_eq = V_T/R₁ + V_T/R₂  + V_T/R₃ .. [ as we know V_T = V₁ = V₂ = V₃ ]
  1/R_eq = 1/R₁ + 1/R₂  + 1/R₃ .. (c)

R_eq = Equivalent resistance of the resistors in parallel.
When there are just 2 parallel paths then equation (c) looks like this:
1/R_eq = 1/R₁ + 1/R₂
=>Equivalent resistance in a parallel circuit R_eq = R₁R₂ /( R₁ + R₂ ) (d)

Equivalent resistance formula for a parallel circuit

Equivalent resistance in a parallel circuit of 2 resistances in parallel: R_eq = R₁R₂ /( R₁ + R₂ )

Numerical Problems on equivalent resistance of parallel circuits | Parallel circuit problems with Solutions

1 ]

Two resistors with resistances of 5 Ω and 20 Ω each are connected in parallel to a 16-V battery. Calculate the equivalent resistance of the circuit, the total circuit current, and the current in each branch of the circuit.

Solution
Equivalent resistance = R_eq = (5×20)/(5+20) = 100/25 = 4 ohm
V_T = 16 volts
Total circuit current = V_T / R_eq = 16/4 amp = 4 amps
Current through 5 ohm branch = V_T /5 amps = 16/5 amps = 3.2 amps
Current through 20 ohm branch = V_T /20 amps = 16/20 amps = 4/5 amps=0.8 amps

2 ]

Three resistors of 30 Ω, 15 Ω, and 10 Ω are connected in parallel to a 20-V battery. Calculate the equivalent resistance of the circuit, the total current for the circuit, and the current flowing through each resistor.

Solution
Equivalent resistance:
Let’s first find out the eq resistance of 30 ohms and 15 ohms = (30×15)/(30 +15) ohm= (30×15)/(45) ohm = 10 ohm
Then we will find out the final eq resistance by using the above-derived resistance 10 ohms and the 3rd resistance (another 10 ohms again) = (10×10)/(10 + 10) ohm =100/20 ohm = 5 ohm
so R_eq = 5 ohm
V_T = 20 volts
Total circuit current = V_T / R_eq =20/5 Amps = 4 A
Current through 30 ohm path = 20/30 A=2/3 A
Current through 15 ohm path = 20/15 A = 4/3 A
Current through 10 ohm path = 20/10 A = 2 A

Ohm’s Law Numerical problem worksheet – test your preparation

Ohm’s Law – Read the fundamentals