Numericals on series and parallel combination of resistors class 10
In this post, we have solved a set of Numericals on series and parallel combinations of resistors for class 10 physics.
Formulas Used
Resistors in series: Req = R1 + R2 + R3
Resistors in parallel: 1/Req = 1/R1 + 1/R2 + 1/R3
Numericals on series and parallel combination of resistors for class 10
Question 1) If five resistances, each of value 0.5 ohm, are connected in series, what will be the resultant resistance?
Solution:
As per the law of combination of resistances in series,
R=R1+ R2+ R3+ R4+ R5
R=0.5+0.5+0.5+0.5+0.5=2.5 ohm.
Question 2) If 5 resistances of 5 ohm each are connected in parallel, what will be their total resistance?
Solution:
1/R = 1/5 +1/5 + 1/5 +1/5 + 1/5 = 5/5 = 1 ohm
=> R = 1/1 ohm = 1 ohm
Equivalent resistance = 1 ohm
Question 3) Show how you would connect two 4 ohm resistors to produce a combined resistance of
(a) 2 ohms
(b) 8 ohms.
Solution :
(a) By connecting in parallel:
Since equivalent resistance will be
1/ R = 1/4 + 1/4 = 2/4 = 1/2
Therefore, R = 2 ohm
(b) By connecting in series:
Since equivalent resistance will be
R = 4 ohm + 4 ohm = 8 ohm.
Question 4) A wire that has resistance R is cut into two equal pieces. The two parts are joined in parallel. What is the resistance of the combination?
Solution :
The resistance of each part is R/2.
These parts are joined in parallel.
Equivalent resistance Req is given by
1/Req = 1/[R/2] + 1/[R/2]
=>1/Req= 2/R+2/R
Req=R/4. [answer]
Question 5) A battery of 9 V is connected in series with resistors of 0.2 Ω, 0.3 Ω, 0.4 Ω, 0.5 Ω, and 6 Ω. How much current would flow through the 6 Ω resistor?
Solution:
V = 9 V
Req =.2 +.3 + .4 + .5 + 6 ohm =7.4 ohm
As these resistors are in series, same current will flow through all of these.
current I =V/Req =9/7.4 A = 1.22 A
Question 6) An electric bulb of resistance 30 Ω and a resistance wire of 4 Ω are connected in series with a 6 V battery. Calculate :
(a) total resistance of the circuit.
(b) current through the circuit.
(c) potential difference across the electric bulb.
(d) potential difference across the resistance wire.
Solution:
a) Total resistance R = 30 + 4 = 34 ohm
b) V = 6 V
Current through the circuit = I
I = V/R = 6/34 =0.176 A
c) Pd across the electric bulb = I Rbulb = 0.176 x 30 V = 5.29 V
d) Pd across the resistance wire =Battery emf – drop across bulb= 6 – 5.29 = 0.71 V
Question 7) A 4 Ω coil and a 2 Ω coil are connected in parallel. What is their combined resistance ? A total current of 3 A passes through the coils. What current passes through the 2 Ω coil ?
Solution:
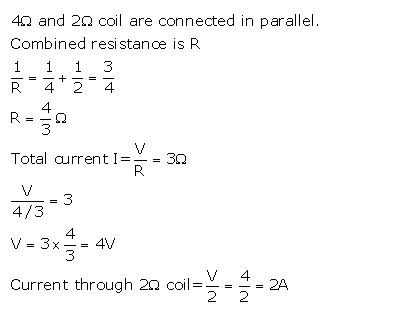
Question 8) Two resistances when connected in parallel give the resultant value of 2 ohm; when connected in series the value becomes 9 ohm. Calculate the value of each resistance.
1/R1 + 1/R2 = 1/2
=> 2 = R1R2/[R1 + R2]
=> 2[R1 + R2] = R1R2 ……….. (1)
R1 + R2 = 9 …… (2)
from (1) and (2) we get: 2×9 = R1R2
=> R1R2 = 18
=> R1 = 18/R2 ……..(3)
from (2) & (3)
18/R2 + R2 =9
=>18 + R22 =9R2
=>R22 -9R2 + 18 = 0
Solving: R2 = 3 or 6
When R2 = 3, then from equation (2) we get R1 = 6
When R2 = 6, then from equation (2) we get R1 = 3
So two resistances are 6 ohm and 3 ohm.
Question 9) A resistor of 8 ohms is connected in parallel with another resistor X. The resultant resistance of the combination is 4.8 ohms. What is the value of the resistor X?
Solution:
1/8 + 1/X = 1/4.8
=>1/X = 1/4.8 – 1/8 = 3.2/[4.8×8]
=>X = 4.8×8/3.2=12 ohm
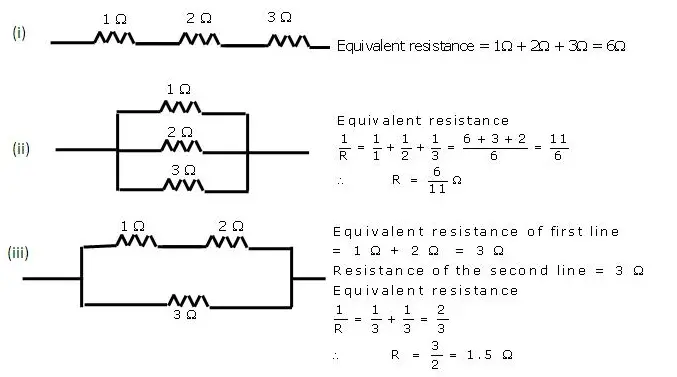
Question 10) You are given three resistances of 1,2 and 3 ohms. Show by diagrams, how with the help of these resistances you can get:
(i) 6 Ω (ii) 611 Ω (iii) 1.5 Ω
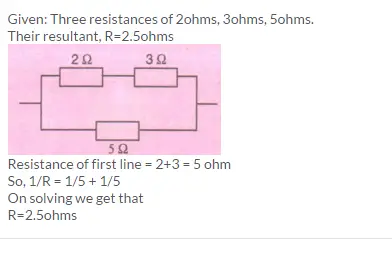
Question 11) How will you connect three resistors of 2 Ω, 3 Ω, and 5 Ω respectively so as to obtain a resultant resistance of 2.5 Ω? Draw the diagram to show the arrangement.
Question 12) How will you connect three resistors of resistances 2 Ω, 3 Ω, and 6Ω obtain a total n si stance of: (a) 4 Ω., and (b) 1Ω?
Solution :

