Relation between resistance and resistivity through a simple experiment
Last updated on June 6th, 2022 at 09:45 pm
In this post, we will cover How to find the Relation between resistance and resistivity through a simple experiment. It’s basically deriving the resistivity formula with our understanding of electrical resistance. Once we derive the equation or formula of resistance, the definition, symbol, and formula of resistivity will be prominent to us.
To do this we will use an easy and fundamental experimental setup. We will also see how the formulas of resistance and resistivity come up with the help of this simple experiment.
So let’s begin.
Experimental setup to derive the formulas of resistance & resistivity | find the Relation between resistance and resistivity with an experiment
In this experiment, the factors that affect the resistance of a wire can be investigated using a 1m length of 32 swg (diameter 0.2743 mm) nichrome wire taped to a meter rule, as in figure 1. [swg stands for Standard Wire Gauge]
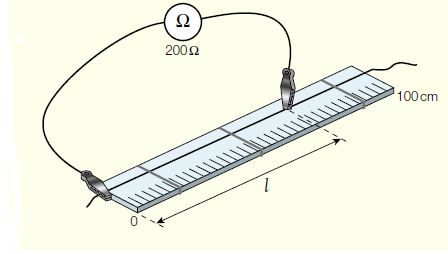
For the purpose of this experiment, it is easier to measure the resistance of the wire directly using an ohmmeter set on its 200Ω range, as shown in Figure 1.
One crocodile clip is kept fixed at the zero end of the wire, while the other is pressed firmly on the wire to make contact at different lengths along the wire.
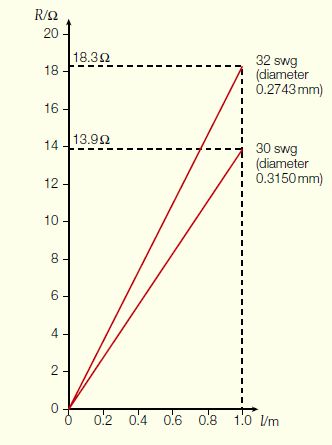
The corresponding resistance, R, for each length, l, is recorded, and a graph of R against l is plotted. A typical set of results has been plotted in Figure 2.
The figure also shows the graph for a length of 30 swg (diameter 0.3150 mm) nichrome wire.
Observation
What can we deduce from these graphs?
1) Firstly, as they are both straight lines through the origin, it is obvious that:
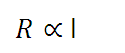
2) The second deduction requires some calculation. The ratio of the areas of the cross-section of the two wires is:
A30/A32 = 0.31502/0.27432 =1.32 [ since A = πd2/4 ]
The corresponding ratio of the resistances of a 1m length of each wire is:
R30/R32 = 13.9 Ω/18.3 Ω = 0.76 = 1/1.32
In other words,
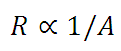
From the experiment, we can see that for a conductor (for example, a wire) of length l and uniform area of cross-section A: resistance is directly proportional to the length and inversely proportional to the cross-sectional area of the conductor.
If we think about this observation, this makes sense: if the wire is longer, it will be more difficult for the electrons to drift from one end to the other. (resistance is more)
And If the wire has a larger cross-sectional area, it will be easier for the electrons to flow (less resistance like water flow through a larger diameter pipe).
deriving the formula of resistance
Combining the two relationships above:
we get:
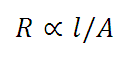
Hence, R = ρ l / A …………(1)
ρ is a constant and is a property of the material of the wire known as resistivity.
So we can say, resistivity has a symbol ρ (‘rho’).
And the equation (1) above gives us the formula of resistance and the relationship between resistance and resistivity.
What we get from the equation of resistance? | Three Things Determine Resistance
If you think about a nice, simple electrical component, like a length of wire, its resistance depends on:
1) Length (l). The longer the wire the more difficult it is to make a current flow.
2) Area (A). The wider the wire the easier it is to make a current flow.
3) Resistivity ( ρ ). This depends on the material the wire’s made from, as the structure of the material may make it easy or difficult for a charge to flow. In general, resistivity depends on environmental factors as well, like temperature.
Equation or formula of resistivity:
From the equation or formula of resistance we derived above, we get the formula of resistivity: ρ = RA/l …………………..(2)
And the unit of resistivity ρ is Ohm-metre
From this equation, we also find out how resistance and resistivity are related.
Also, check this related post to find the Resistivity of different materials.

