Series Circuits, Resistors in series & equivalent resistance formula & numerical

Last updated on April 20th, 2023 at 04:07 pm

In this post, we will study simple series circuits with the help of a series circuit diagram. We will also go through related topics like resistance in series or resistors in series, series circuit formula of equivalent resistance, etc. This post also covers series circuit numerical problems with solutions.

Series circuit | resistance in series | resistors in series

What is a series circuit? A series circuit consists of several resistors connected in sequence, one after the other. This increases the length of the conductor. Therefore total resistance increases as the number of resistors in series are increased in the circuit.

A series circuit is also referred to as resistance in series or resistors in series.

Series Circuit Diagram (a simple one)

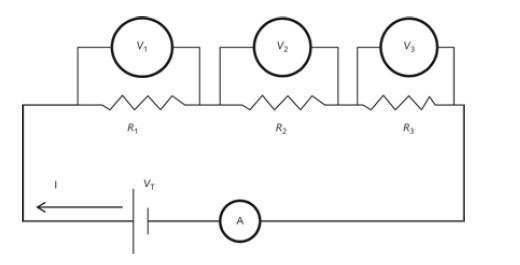
In the above, series circuit diagram three resistors R1, R2, and R3 are connected in sequence, one after the other. In other words, these are connected in series.

Characteristics of Series Circuit as found from experiments

Experiments show that the current in the series circuit made up of one loop is the same everywhere.

As there are potential drops across each resistor, the total voltage across the battery is equal to the sum of the potential drops across each resistor.

If one resistor goes out, then the whole circuit goes off. (like when a light bulb in a series circuit goes out, the entire circuit becomes inoperative)

Equivalent Resistance of a series circuit | series circuit formula of equivalent resistance

Using Ohm’s Law and our experimental results, we find that: (see the circuit diagram above)

The current flowing through the circuit = I = current through each of the resistors in series
I = I₁ = I₂ = I₃
V_T = Total voltage or Potential difference
R_eq = V_T/I = equivalent resistance

V_T = V₁ + V₂ + V₃ = sum of potential drops across each resistor

R_eq =  V_T/I = (V₁ + V₂ + V₃) /I = V₁/I + V₂/I + V₃/I = V₁/I₁ + V₂/I₂ + V₃/I₃ = R₁ + R₂ + R₃

Series circuit formula of equivalent resistance R_eq = R₁ + R₂ + R₃

Series circuit numerical problems with solutions | Numerical Problems (based on series circuit and its equivalent resistance)

1] Resistors of 10 Ω, 15 Ω, and 5 Ω are all connected in series to a 90 V source of potential difference. Calculate the total equivalent resistance of the circuit, the total current in the circuit, and the potential drop across each resistor.

Solution:
Equivalent Resistance = Req = (10 + 15 + 5) Ω = 30 Ω
Total current in the circuit I = V/Req = 90 V/ 30 Ω = 3 Ampere

The potential drop across each resistor:
Potential drop across 10 Ω resistor = I x resistance = 3 x 10 V = 30 V

Potential drop across 15 Ω resistor = I x resistance = 3 x 15 V = 45 V

Potential drop across 5 Ω resistor = I x resistance = 3 x 5 V = 15 V

2] Three resistors of 50 Ω, 30 Ω, and 40 Ω are connected in series to a 60 V battery. Calculate the equivalent resistance of the circuit, the total current in the circuit, the total power generated by the circuit, and the voltage drop across the resistors.

Solution:
Equivalent Resistance = (50 + 30 + 40) Ω = 120 Ω
Total current = I = V/R = 60/120 Ampere = 0.5 A [ we used Ohm’s law here]
Total power = P = VI = 60 x 0.5 Watt = 30 W
Voltage drop across 50 Ω = IR =0.5 x 50 V= 25 V
Voltage drop across 30 Ω = IR = 0.5 x 30 V = 15 V
Voltage drop across 40 Ω = IR = 0.5 x 40 V = 20 V

3] Fifteen resistors with equal resistance are connected in a series circuit. if the voltage and current are equal to 120 v and 1.5 amp, respectively, determine the individual resistance of each resistor.

Solution:
Say, the individual resistance of each resistor is R.
Hence, the equivalent resistance of 15 such resistors in a series circuit is R_eq=15R
V = 120 V
I = 1.5 A
Using Ohm’s law:
V = IR_eq
=> R_eq = V/I = 120/1.5 = 80 ohm
15R = 80
=>R = 80/15 = 5.33 ohm

Formula Used to solve the series circuit numerical problems

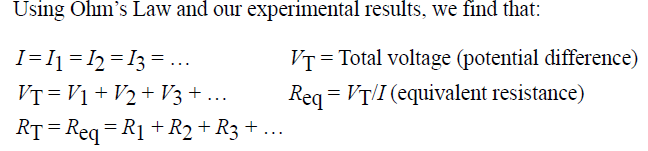
Related Posts
Ohm’s Law
Ohm’s Law Numericals