Numerical problems based on the inclined plane physics – solved
Last updated on April 15th, 2021 at 01:50 pm
In this post, we will focus on numerical problems based on inclined plane physics. We will list down the problems and solve them one by one.
Numerical problems based on the inclined plane physics
1] A 5-kg mass, initially at rest, slides down a frictionless 30° incline. Calculate the force parallel to the incline and the acceleration of the mass. If the incline is 0.8 m long, calculate the velocity of the mass when it reaches the bottom of the incline.
1] solution:
The goal of the problem is to calculate the desired quantities of force, acceleration, and velocity parallel to the incline (when friction is neglected).
The force parallel to the incline =F= mg sin θ = (5) (9.8) sin 30 = 24.5 N downwards.
Acceleration of the mass =a= g sin θ = (9.8) sin 30 = 4.9 m/s2 downwards
say the velocity of the mass when it reaches the bottom of the incline V and we have to find it out. Then we can use the formula like this:
V2 = U2 + 2 a S
(Here, U =0, acceleration a = 4.9 m/s2 and S = 0.8 m)
So, V = (2 a S)1/2 = (2 x 4.9 x 0.8)1/2 = 2.8 m/s
2 ] A 2-kg mass is sliding down an incline with an unknown angle, as shown. The incline is assumed to be frictionless and is 1.2 m long. The mass starts from rest and is observed to take 2.3 s to reach the bottom. What is the angle of the incline?
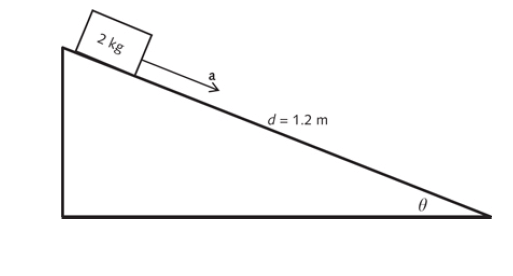
Acceleration of the mass along the incline a = g sin θ = 9.8 sin θ …… (1)
We need to use this formula: S = Ut + (1/2) a t2
As, U = 0, the formula becomes: S = (1/2) a t2
=> a = (2 S)/ t2 = (2 x 1.2) /2.32 = 0.45 m/s2 …. (2)
Now from equation 1 and 2:
0.45 = 9.8 sin θ
=> sin θ = 0.45/9.8 = 0.046
=> θ = 2.63 degrees
