Banking Angle & Banked Curve | Banking angle formula Derivation
Last updated on April 20th, 2023 at 11:29 am
In this post, we will discuss the concepts of the Banking Angle & Banked Curve. Then we will study the Banking angle formula and perform the derivation of the Angle of Banking formula.
Banking Angle & Banked Curve
So, let’s see what the banking angle is and why it is so important.
When a car travels without skidding around an unbanked curve, the static frictional force between the tires and the road provides the centripetal force. But the wear and tear of tires caused by this friction increases the maintenance cost of the vehicles and increases the risk of sudden accidents at the curved points of the roads.
However, if the curve of a road is banked at an angle relative to the horizontal, much in the same way that a plane is banked while making a turn, the reliance on friction to provide the required centripetal force can be eliminated completely for a given speed. This angle the curve of the road makes here with respect to the horizontal is called banking angle or banked angle.
Benefits of Banked curves and Banking angle: The banking angle at the curved turns of the roads (or Banked curves) reduces friction between the tires and the road and this, in turn, reduces maintenance costs and accidents of the vehicles.
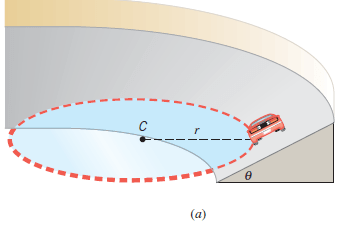
banking angle is θ, and the center of the circle is at C.]
Banking angle formula with derivation | derive an expression for angle of banking
Figure (a) shows a car going around a friction-free banked curve. The radius of the curve is r, where r is measured parallel to the horizontal and not to the slanted surface.
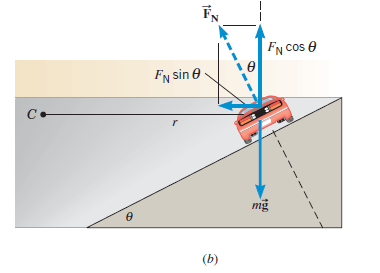
Figure (b) above shows the normal force FN that the road applies to the car, the normal force being perpendicular to the road.
Because the roadbed makes an angle θ with respect to the horizontal, the normal force has a component FN sin θ that points toward the center C of the circle and provides the centripetal force:
Fc = FN sin θ = (mv2)/r ……… (1)
The vertical component of the normal force is FN cos θ and, and since the car does not accelerate in the vertical direction, this component must balance the weight mg of the car.
Therefore, FN cos θ = mg …… (2)
Dividing equation 2 by equation 1 shows that:
(FN sin θ)/(FN cos θ) = [(mv2)/r]/mg
=> tan θ = v2/(rg) ...……………………… (3). This gives the equation or formula of the Banking angle.
And thus we can derive the banking angle formula.
Banking Angle of the Road
1 ) Equation 3 indicates that, for a given speed v, the centripetal force needed for a turn of radius r can be obtained from the normal force FN by banking the turn at an angle θ.
2 ) This banking angle is independent of the mass of the vehicle. The formula doesn’t contain any mention of the mass m in it.
3 ) Greater speeds and smaller radii require more steeply banked curves—that is, larger values of θ.
4 ) At a speed that is too small for a given θ, a car would slide down a frictionless banked curve.
5 ) At a speed that is too large, a car would slide off the top.
Suggested Reading:
Centripetal force formula
Centripetal force and washing machine
