Numerical problems based on the efficiency of machines

In this post, we will first find out what the efficiency of a machine means, and then we will solve numerical problems using the concept and formula of the efficiency of machines.

If a machine, such as an electric motor, is used to raise a load, electrical energy must be provided to the motor. This is the input energy to the motor. The motor uses some of this energy to do the useful work of raising the load. But some of the input energy is used to overcome frictional forces and therefore gets converted to thermal energy.

So the ratio of useful energy output and actual energy input or the ratio of useful power output and actual power input is less than 1.

This ratio is called the efficiency of the machine.

The formula of the efficiency of a machine = useful energy output / actual energy input = useful power output / actual power input

Numerical problems for efficiency calculation

1 ) Suppose that a body is being pulled up by 20 m along a rough inclined plane with constant speed. The mass is 15 kg and the angle of the incline is 45°.

There is a constant frictional force of 42 N opposing the motion. Find out the efficiency with which the force raised the mass.

Solution:

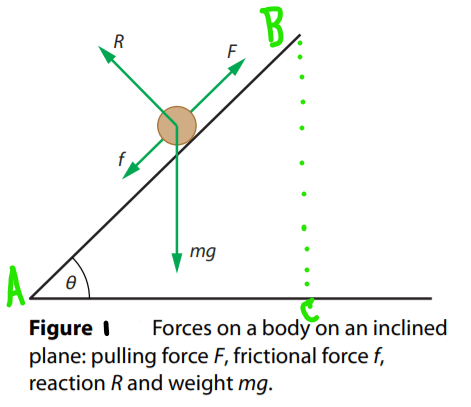
The forces on the body are shown in Figure 1. Since the body has no acceleration, we know that:
R = mg cos θ = 106.1 N
F = mg sin θ + f = 106.1 + 42 = 148.1 N ≈ 150 N
Let the force raise the mass a distance of 20 m along the plane. The work done by the force F is:
W = 148.1 × 20 J
W = 2960 J

AB = 20 m

Effective height gain = BC = AB Sin 45° = 20 Sin 45° = 14.1 m

The force effectively raised the 15 kg by a vertical height of 14.1 m.

So the force increased the potential energy of the mass by mgh = 2121 J.

The efficiency with which the force raised the mass is thus:

efficiency = 2121/2960
efficiency = 0.72 = 72 %

2 ) A 0.50 kg battery-operated toy train moves with constant velocity 0.30 m s⁻¹ along a level track. The power of the motor in the train is 2.0 W and the total force opposing the motion of the train is 5.0 N.
a) Determine the efficiency of the train’s motor.
b) Assuming the efficiency and the opposing force stay the same, calculate the speed of the train as it climbs an incline of 10.0° to the horizontal.

Solution

a) The power delivered by the motor is 2.0 W. Since the speed is constant, the force developed by the motor is also 5.0 N.

The power used in moving the train is Fv = 5.0 × 0.30 = 1.5 W.

Hence the efficiency is:
total power out/total power in =1.5 W/2.0 W = 0.75
The efficiency of the train’s motor is 0.75 (or 75%)

b) The component of the train’s weight acting down the plane is mg sin θ and the force opposing the motion is 5.0 N.

Since there is no acceleration (constant velocity), the net force F pushing the train up the incline is:
F = mg sin θ + 5.0
F = 0.50 × 10 × sin 10° + 5.0
F = 5.89 N ≈ 5.9 N

Thus:
efficiency = 5.89 ×v/2.0

But from part a the efficiency is 0.75, so:
0.75 = 5.89 ×v/2.0
⇒ v =2.0 × 0.75/5.89
v = 0.26 m s⁻¹